CCF20090422007

Zróżnicowanie szkół i oddziałów ze względu na wybrane cechy społeczne uczniów

Zanim przejdziemy do analizy procedur rekrutacji uczniów do szkoły i podziału ich na oddziały klasowe, przyjrzyjmy się globalnemu oszacowaniu efektu segregacji międzyszkolnych i międzyoddzia-łowych. Zacznijmy od efektu segregacji ze względu na SES ze względu na opozycję miasto-wieś. Efekt ten przedstawia poniższy wykres.

Wykres 1

Procentowe rozkłady SES rodziny pochodzenia ucznia w szkołach miejskich i dużych wiejskich

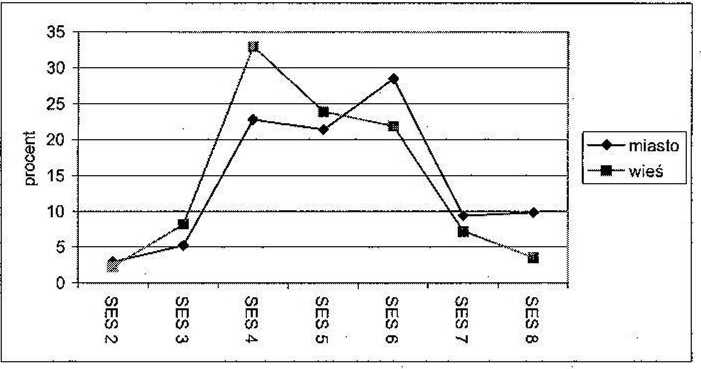
Analiza wariancji (ANOVA) wskazuje, że podział miasto - wieś wyjaśnia niespełna 2% zmienności wskaźnika SES. To niewiele, ale pamiętajmy, że próbka szkół wiejskich reprezentuje tylko duże szkoły.

Czy oznacza to, że szkoły podstawowe w Polsce pracują w stosunkowo mało zróżnicowanych warunkach społecznych? Oczywiście, nie. W próbce miejskiej ANOVA wykazuje, że szkoła jako zmienna niezależna wyjaśnia 6,3% wariancji wskaźnika SES, w próbce wiejskiej - 4,4%. Podział na oddziały szkolne wyjaśnia znacząco więcej. W próbce miejskiej - 16,0%, w próbce wiejskiej 8,3% wariancji wskaźnika SES. Efekt segregacji między oddziałowej jest więc znacznie silniejszy niż wskaźnik segregacji międzyszkolnej. Oznacza to, że za zróżnicowanie składu społecznego poszczególnych oddziałów odpowiadają w znacznym stopniu szkoły i stosowane przez nie procedury podziału uczniów na oddziały klasowe.

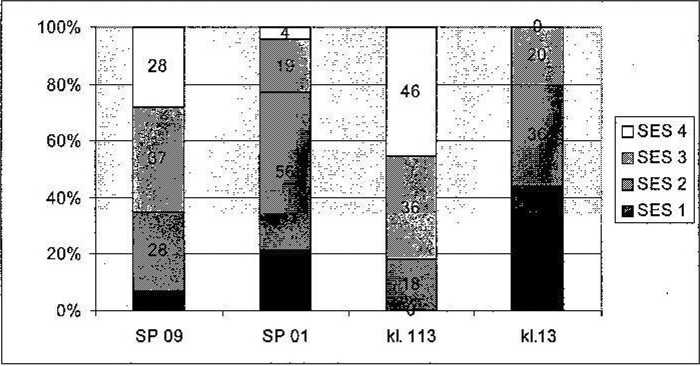
By lepiej zdać sobie sprawę z wielkości różnic w składzie społecznym szkół i oddziałów, przytoczmy charakterystyki skrajnych przypadków. Zacznijmy od środowiska miejskiego. Ranking otwiera szkoła podstawowa o numerze kodowym 09 ze średnią wskaźnika SES 5,9 pkt. Na dole rankingu znajduje się szkoła 01 ze średnią 4,4 pkt. Kontrastowe oddziały natomiast to klasa o numerze 113 ze średnią 6,5 pkt i klasa o numerze 13 ze średnią wskaźnika SES 3,8 pkt. Wykres 2 ilustruje te kontrasty za pomocą rozkładu 4-punktowego wskaźnika SES.

Wykres 2

Szkoły i oddziały o najkorzystniejszym i najmniej korzystnym składzie społecznym w próbce miejskiej