CLEBSCH 2

Rys. 8-12

a)

b)

i

-X-

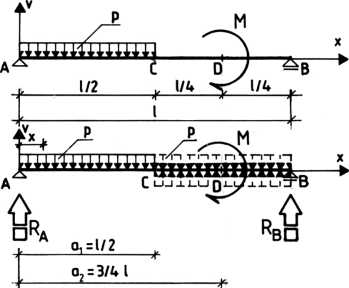
Rys. 8-13

belek jednoprzęsłowych o stałej sztywności El, przy czym uwzględnia się niżej podane warunki.

1.    Początek układu współrzędnych przyjmuje się na jednym z końców belki (rysunek 8-13a).

2.    Równanie momentu zginającego M_a na wszystkich odcinkach belki zapisuje się uwzględniając siły działające po jednej stronie przekroju, przy czym wszystkie wyrazy w równaniu M_a dotyczącym odcinka poprzedniego muszą być uwzględnione bez zmian w równaniu M_x odcinka następnego. W wypadku obciążenia ciągłego, kończącego się w określonym punkcie belki (np. punkt C na rys. 8-13b), niezbędne jest więc „przedłużenie” tego obciążenia do końca belki (na odcinku CB) i jednoczesne dodanie na tym odcinku obciążenia równoważącego (o zwrocie przeciwnym).

3.    Wszystkie nowe wyrażenia wchodzące do równania M_x rozpatrywanego odcinka muszą zawierać mnożnik (x — a_i), gdzie x — odcięta danego przekroju, a_t — odcięta punktu początkowego danego odcinka.

4.    Całkowanie wyrażeń zawierających dwumiany (x — a_{) należy wykonać względem nowej zmiennej (jc — a_t), czyli bez otwierania nawiasów, zgodnie z regułą

(8-24)

( v- /i _t    1

J (x-a_i)^mdx = J (x-a_i)d(x-a_i)^m = —— + C.

5.    Stałe całkowania, jako wspólne dla wszystkich odcinków, pisze się na początku prawej strony równań.

6.    Równanie M_a zapisuje się od razu w odniesieniu do całej belki w takiej postaci, aby pionowymi kreskami z odpowiednimi indeksami były zaznaczone granice odcinków zmienności M_x.

7.    Jeżeli w równaniu M_a występuje moment skupiony M, to przy tym momencie zapisuje się mnożnik (x — a,)⁰, gdzie a_t — odcięta punktu przyłożenia momentu skupionego M.