467 (12)

467

13$. Ruch ptaki ciało sztywnego

Dwa bloki A i B o musach nt\ im< i promieniach ?*| i rj są PRZYKŁAD 15.8

owinięte nieważki) niero/ciąiiliwą nicią, Nić jest przerzucona

przez blok C o musie w» i promieniu r\. Blok ten może

obracać się bez tarciu wokot po/umiej osi 0\. Zakładając, że

nić nie ślizga się po bloku C\ znaleźć przyspieszenie środków

Oi i 02 bloków A i H ora/ przyspieszenie kątowe bloku C

(rys. 15.10).

C

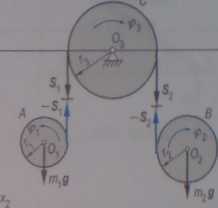
RYS, 15.10

ROZWIĄZAŃ!!

Po rozdzieleniu układu nu trzy układy proste otrzymamy równania ruchu

iA^!i ** wi \$ - S\ Iq\$[ ^m S\t\ lo_sif>i *=» S;ry - S\>\

/Mjjfj m - 5;

gdzie ić| i Jc2 oznacząją odpowiednio przyspieszenia środków mas bloków A i B, czyli punktów 0\ i 0;. Z równań więzów wynikają jeszcze dodatkowo dwu równania

jfj » riv’i — r\fa A’2 = F2ęVj + rsfa

Po rozwiązaniu układu równań dostaniemy

6(wi| + mi) + 2ni2

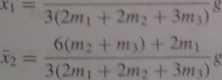
2(»*2 — r«i)

(2m\ + 2/«2 + 3mj)rj

Jeżeli mamy do czynienia z układem o jednym stopniu swobody, korzystnie jest stosować metody energetyczne. Pokażemy to na przykładach.

Deska AB o masie M leży nu dwóch jednakowych jedno- PRZYKŁAD 15.9

rodnych wałkach. Końce deski są przymocowane do sprężyn

jptpspółczynniku sztywności c. Zakładając, że wałki nie

fliz gają się po podłodze, a deska po wałkach, znaleźć okres

drgań okładu, jeżeli masa każdego wałka jest równa m

(rys. 15.11).