m305

ułamki łańcuchowe

305

43

T9

2 +

2+

z niedomiarem danej liczby dodatniej otrzy-~ - e się z rozwinięcia dziesiętnego tej liczby rczez odrzucenie wszystkich cyfr występujących za prawo od wybranej cyfry. P. dz. z nadmiarem —r» skuje się przez analogiczne odrzucenie cyfr, a “wd epnie przez powiększenie o 1 ostatniej pozbawionej cyfry (jeśli tą ostatnią cyfrą jest 9, to ^asiępuje się ją przez 0 i powiększa się o 1 poprzednią cyfrę, przy czym jeśli i tą poprzednią jest 9, to zastępuje się ją przez 0 itd.). P. dz. powstałe przez odrzucenie cyfr poczynając od - i >-szej po przecinku dziesiętnym różni się :o danej liczby mniej niż o 10 ". Zazwyczaj przyjmuje się p. dz. z niedomiarem, gdy pierwsza z odrzucanych cyfr jest mniejsza od 5, natomiast p -z. z nadmiarem, gdy pierwsza z odrzucanych eytr jest nie mniejsza od 5.

.-ktmki łańcuchowe, ułamki ciągłe, wyrażenia postaci: arytmetyczne można zapisać w sposób skrócony następująco: [a;a_l,a₂₉a₃,...']. Na przykład:

[2; 3,1,4].

3 +

1 +

Każdą liczbę wymierną można rozwinąć na u ł. arytmetyczny skończony. Każdą liczbę niewymierną można przedstawić w postaci u.ł. nieskończonego. Na przykład:

5^{1 2}

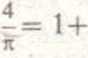
7²

2+

c= 2-ł-

2+

3+

+-

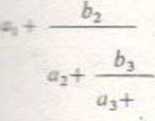
41+

- ? dla zaoszczędzenia miejsca zapisuje się leż następująco:

4-t-

5-4-

gdzie e jest podstawą logarytmów naturalnych. Liczby niewymierne będące pierwiastkami drugiego stopnia dadzą się przedstawić w postaci u.ł. arytmetycznych nieskończonych i okresowych. Na przykład:

y/2 = [1; 2,2,2,...],

yn = [3; 1,1.1,1,6,1,1,1,1,6....].

Uważa się, że u.ł. pierwszy wprowadził w XVI w. matematyk wł. R. Bombclli. Prace nad teorią u.ł. /.apocząikował w XVII w. matematyk wL P. A. Cataldi, a do rozwoju tej teorii przyczynili się matematycy ang. J. Wallis i W. Brouncker, matematyk hol. Ch. Huygens, matematyk szwajc. L. Euler, matematyk nicm. J. H. Lambert, matematycy franc. J. L. de Lagrange i A. M. Le-gendrc oraz matematyk hol. T. J. Stieltjes.

Notatka z dziennika naukowego C. F. Gaussa z 24 V 1796. Przedstawione są dwa szeregi nieskończone zapisane za pomocą ułamków łańcuchowych.

1

—    ...+M+^+....

mi *2    l"3    k-i k

g~zse j jest liczbą całkowitą, a_k, b_k są liczbami sacuralnymi, przy czym k = l,...,w lub A: = 1,2...

jeśżi ż = 1.....w, wówczas u.ł. nazywa się u.ł.

2

kończonymi. Jeśli 1, dla k= 1,..., #i, wówczas uł nazywa się u.ł. arytmetycznymi. U.ł.