MAT23

23

Stosując wzór na całkowanie przez podstawienie, obliczyć

4

1. f ~^ŚL-

J 1+/? 0 I

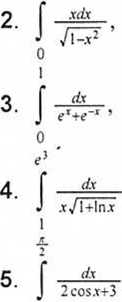
o

In 2

6.    | Je^x - 1 dx,

o

4

7.    J xjx² + 9 dx. o

10.    Twierdzenia o wartości średniej dla całek oznaczonych

b

Def. Jeżeli f e L([a,b]), to liczbę H[f] :=    [ /(.v)r/.Y nazywamy średnią całkową funkcji/w

a

przedziale [a,b].

Pierwsze twierdzenie o wartości średniej dla całek. Jeżeli fg e L([a,b]),f ma stały znak w przedziale [a, b] oraz g ma własność Darboia w [a,b], to

b    b

V J/fcOsfrkk = #(0\Ax)dx.

Drugie twierdzenie o wartości średniej dla całek. Jeżelif jest monofoniczna w [a, 6] oraz g e L([a,b]), tof-g € L([a,b]) oraz

b    c    b

V    = /(«) }g{x)dx +f{b) |g(x)dx.

11.    Całka niewłaściwa, kryteria zbieżności całki niewłaściwej

Zakładamy, że funkcja rzeczywista/jest określona na przedziale [a,b[ a R i całkowalna (w sensie Riemanna) na każdym przedziale [a, fi] c [a,b[. Punkt b nazywamy punktem osobliwym funkcji f gdy b = +co albo b e R, ale/jest funkcją nieograniczoną w pewnym sąsiedztwie punktu b.

Jeśli b jest punktem osobliwym funkjci/oraz istnieje granica właściwa

Opracował: Marian Malec