Scan10021

TWIERDZENIE

Każda liczba zespolona zfO posiada dokładnie n różnych pierwiastków określonych

wzorem:

cos-

0+2kn .. ę>+2«n ]

-+żsin---L k = 0,L2_____n—\\

Interpretacja geometryczna pierwiastków

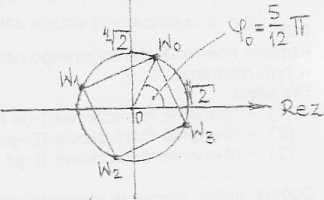
Wszystkie pierwiastki ieżą na okręgu o S(0,0) i R= yl - i i są wierzchołkami n-kąta *re—ego wpisanego w ten okrąg.

PRZYKŁAD

4n

= cos-

. 4n z sin—— 3

2. '_v’l —'/3Ż =?

zpltt ! z |= 2, ęj = 2n--=-n

w0 = ' ,^!2 • I	cosł-n+isin—n 1
^0 1 4J f	< 12	12 ) .. nłi
w, = 4/2-	cos—n-f	ism- n
V	12	12 J
x /2	r i?	. . 17_
w, = 4/2 •	cos—n	+ rsm—n
	V 12	12 23 'j
	f 03
4 /a i w3 = •	cos;—n-	fisiu—II
	l 12	12 J

WMomian zmiennej zespolonej

Wielomianem stopnia n w dziedzinie zespolonej nazywamy wyrażenie postaci:

W_n{z) - a.₀ + GjZ + a₂z² +... + a_nzⁿ