2192973021

Oczywiście, jedynym pierwiastkiem n-tego stopnia z liczby 0 jest 0.

Twierdzenie 5 Niech liczba zespolona z, różna od zera, ma postać z = r(cos (j) + i sin 0).

Wtedy każda liczba w_k, mająca postać

Wk =

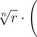
cos

ó + 2kir . ó + 2kn --h i sm-

n

n

gdzie k jest liczbą całkowitą, jest pierwiastkiem n-tego stopnia z liczby z oraz każdy pierwiastek n-tego stopnia z liczby z jest jedną z liczb w_k-

Zauważmy, że różnych pierwiastków n-tego stopnia z liczby z jest n. Są to liczby Wk, gdy k jest jedną z liczb 0, 1,..., n — 1. Wynika to z okresowości funkcji sin i cos.

Przykład 5 Znajdźmy pierwiastki Ą-tego stopnia z liczby 1.

Ponieważ 1 = 1- (cosO + isinO), więc pierwiastkami czwartego stopnia z liczby 1 są liczby, mające postać

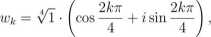
gdzie k jest liczbą całkowitą,

zatem różnymi pierwiastkami czwartego stopnia są:

Wq = 1, W\ = i, W2 = —1, W3 = —i.

Przykład 6 Znajdźmy pierwiastki 3-go stopnia z liczby 8-1-81

Ponieważ

więc pierwiastki 3-go stopnia z tej liczby mają postać

w_k =

₃r= ( t + 2kn V vT28 • ( cos -—--

-I- żsin

f + 2kn\

10