skan ksi ka fizyka

RUCH OBROTOWY

RUCH OBROTOWY

Zadanie 2.51

moment siły hamującej

Jaką silą należy przycisnąć klocek hamulcowy do powierzchni kola rozpędowego o momencie bezwładności / i promieniu R, aby zatrzymać je po upływie czasu /, jeżeli wiruje ono z prędkością kątową u)₀? Współczynnik tarcia wynosi/.

WZORY:

10.3,21.4

Dane:    I, R, o)₀,/

Szukane: F = ?

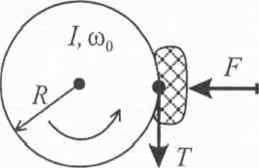
Dociskanie klocka hamulcowego silą F do obracającego się kola powoduje powstanie siły tarcia T = f-F hamującej ruch kola. Silą tarcia działa stycznie do obwodu koła oraz przeciwnie do kierunku jego obrotów. Hamowanie ruchu obrotowego kola opisane jest drugą zasadą dynamiki dla mchu obrotowego, którą w tym przypadku można zapisać następująco:

™=/<V

Iloczyn TR to moment siły tarcia, / jest momentem bezwładności koła względem osi obrotu, natomiast e^, jest opóźnieniem kątowym mchu kola. Wierny, że wartość c_0|> powinna być taka, aby kolo zatrzymało się po czasie Skorzystajmy więc z równania na prędkość kątową dla mchu jednostajnie opóźnionego:

°=“o-^eo_P'

i stąd:

Przejdźmy teraz do naszej podstawowej zależności podstawiając wyznaczone zależności na siłę tarcia i opóźnienie kątowe:

fFR-I—

i stąd szukana wartość siły F:

_r_ l<»o fRl

/m_n

Ody. Klocek hamulcowy należy przycisnąć silą równą y~-

energia kinetyczna i moment siły hamującej

Zadanie 2.52

Jednorodny walec o masie ni i promieniu podstawy R obraca się jednostajnie dookoła swej osi symetrii z prędkością kątową co. a) Oblicz energię kinetyczną obracającego się walca; b) Oblicz moment stałej siły zatrzymującej walec w czasie t. Obliczenia numeryczne wykonaj dla m = 2 kg, R = 30cm, co = 20rad/s, t = 9s. Moment bezwładności

walca względem osi symetrii wynosi: -imR².    WZORY:

Dane:    m=2kg. R =30cm =0,3m, tn = 20rad/s, r=9s

Szukane: E_k =?- energia kinetyczna:

Mj-l- moment stałej siły (tarcia) zatrzymującej walec.

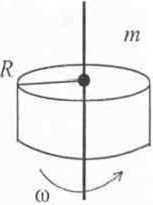
a) Energia kinetyczna obracającej się bryły wynosi:

/<»-

£_k =

(zauważ analogię do wzoru na energię kinetyczną w ruchu postępowym E_v ———. Pamiętaj o tym, żc w ruchu obrotowym

masie m odpowiada moment bezwładności /, a prędkości v -prędkość kątowa co). W naszym przypadku / = ^ mR², czyli:

lcg-m²-y =J s

-mRW ,

£_k =■=-=—m/?² o>²

^k 2    4

Po podstawieniu wartości liczbowych:

ą =—•2-(03)^J-20²J = 1.8 J. 4

b) Moment stałej siły hamującej nich walca My możemy wyznaczyć z drugiej zasady dynamiki dla ruchu obrotowego:

gdzie moment bezwładności walca I = ^niR², natomiast stałe opóźnienie r.^ znajdziemy z równania dla prędkości kątowej w ruchu jednostajnie opóźnionym:

0=co-E_op/ i stąd £_<v=®.

Powracając do wzoru na moment siły hamującej otrzymujemy:

My =-mR²— kg-irr — = kg~-m=N-m 2 t    s s*

87