skan ksi ka fizyka3

RUCH SATELITY W POLU GRAWITACYJNYM

Zauważmy, że zapisane tu równanie jest identyczne z równaniem otrzymanym przy rozwiązywaniu zadania poprzednim sposobem. Zatem w obu metodach otrzymujemy ten sam wynik.

Odp. Prędkość ruchu Księżyca po orbicie kołowej wokół Ziemi równa jest 1000 m/s.

Zadanie 3.3

ruch po orbicie kołowej

Satelita krąży dookoła Ziemi na wysokości /i = 2/?, gdzie R jest promieniem Ziemi. Znajdź prędkość satelity na orbicie mając dane R =6370 km oraz przyspieszenie przy powierzchni Ziemi g = 9,8 m/s³.    WZORY- *

Dane: h = 2R.    F=6370km,    g=9,8m/s^:    24.10.1,10.4

Szukane: v = ? - prędkość satelity na okoloziemskiej orbicie

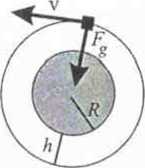
Z treści zadania wynika, ze satelita krąży dookoła Ziemi po orbicie kołowej tak jak na rysunku obok. Na satelitę działa siła grawitacji

„ _ GM m

gdzie G - stała grawitacji, M - masa Ziemi, a m - masa satelity. Silę tę możemy wyrazić przez R i g dane w zadaniu. Korzystamy z tego, żc na powierzchni Ziemi siłę grawitacji Fjd możemy zapisać dwojako:

_ G Mm lub

F_tp='»g-

stąd mamy. że

oraz i dalej

G Mm

R²

GM=gR²

_F - S^R‘^m 8 (R + h)²

Ponieważ siła grawitacji działa na satelitę w kierunku Ziemi, do środka Ziemi, a tym samym do środka okręgu, po którym porusza się satelita, pełni ona rolę siły dośrodkowej F_A. Zgodnie z II zasadą dynamiki powoduje ona przyspieszenie dośrodkowe ci_A satelity

“d =

F,\ =m

R + h

V*

R + li

Porównując wyprowadzone wcześniej wyrażenie na F_t z wyrażeniem na F_A otrzymujemy

gR²m _ m\<² (R + h)² ~ R + h’

a stąd

Po podstawieniu danych liczbowych znajdujemy, że prędkość wynosi 9,8-6,37 I0^b 3

ł.

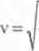
m _ m

7'^m=T

= 4,6*10³ — =4,6—. s s

Odn. Prędkość satelity wynosi 4,6 km/s.

Zadanie 3.4

ruch po orbicie kołowej

WZORY:

24. 10.4, 6.4, 10.1

Sztuczny satelita krąży ze stalą prędkością kątową dookoła Ziemi (promień R) po orbicie kołowej o promieniu r. Obliczyć okres obiegu satelity. Obliczenia numeryczne wykonać dla r = 7938km, R = 6370km i g =9,8m/s³.

Dane:    r = 7938km = 7,938-IO⁶ m

R =6370km = 6370 • 10⁶ m, g =9,8 m/s²

Szukane:

T= ? - okres obiegu satelity

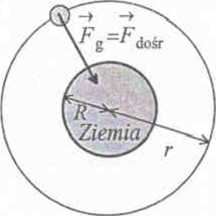
Pomiędzy krążącym wokół Ziemi satelitą a Ziemią działa siła grawitacji o wartości:

^s _ri •

gdzie m jest masą satelity, M - masą Ziemi, r - odległością pomiędzy satelitą a środkiem Ziemi. Siła ta (w układzie związanym z Ziemią) pełni rolę siły dośrodkowej, której wartość można zapisać następująco:

97