skan ksi ka fizyka2

RUCH SATEL

RUCH SATEL

ązanie (zgodne z strony równania

Powyższe równ rysunkiem) to t spierwiastkowa

Po przekształci a po podstawie

Jak widać punl    »zą masę jego siła

przyciągania jest odpowieanto mniejsza.

Odn. Punkt, w którym równoważy się siła przyciągania grawitacyjnego Księżyca i Ziemi leży w odległości x =345600km od Ziemi.

Zadanie 3.2

ruch po orbicie kołowej

Znaleźć prędkość ruchu Księżyca wokół Ziemi zakładając, że jego orbita jest kołowa. Przyjąć, że masa Ziemi \1, = 5,96 IO^:Jkg, odległość między Ziemią a Księżycem

3

r = 3,84 10® m, a stała grawitacji G = 6,6710 ^{11 111}

kgs

2*

WZORY:

24, 10.4

kg-s²

Dane:    M, =5,9610²⁴ kg, r=3,84-10⁸m, (J = 6,6710‘^{n m}

Szukane: v = ? - prędkość Księżyca w ruchu wokół Ziemi

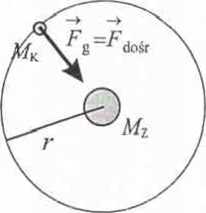
SPOSÓB 1: (siła dośrodkowa)

Gdyby nie było oddziaływania pomiędzy Księżycem i Ziemią, Księżyc poruszałby się po linii prostej (jego ruch nie byłby zaburzony przez obecność Ziemi). Ponieważ jednak występuje między tymi ciałami przyciąganie grawitacyjne, więc Księżyc porusza się po orbicie kołowej wokół Ziemi. Siła grawitacji pełni tu rolę siły dośrodkowej (jest to sytuacja analogiczna do kręcenia długopisem przywiązanym na przykład do sznurówki:

siła przekazana za pośrednictwem sznurówki powoduje, że długopis krąży po torze kołowym). Zatem możemy zapisać następującą równość:

^Fe^=Fioir

Następnie korzystając zc wzoru na silę grawitacji, możemy zapisać:

Z kolei siła dośrodkowa:

dn5r

A/_kv*

Otrzymamy więc następujące równanie:

_cM_zM_k_M_kv

r²    r

r

i stąd:

Po podstawieniu wartości liczbowych:

kg _ nr _i

kgs

t = Jó.67 ■ 10~" ?’⁹⁶ '-⁰0.33 ■ 10⁵ — = 1000 —. v    3,8410* s    s    s

SPOSÓB II: (siła odśrodkowa bezwładności)

Na krążący wokół Ziemi Księżyc działa siła grawitacji, wynikająca ze wzajemnego przyciągania się tych dwócli ciał. Wartość siłv grawitacji wynosi:

f

1 _g -w

r

Siła ta (w układzie odniesienia związanym z krążącym Księżycem) jest równoważona przez silę odśrodkowy bezwładności:

_F

' odir

r

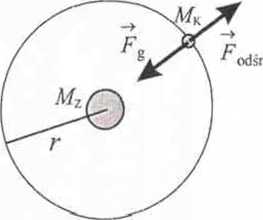
Czyli zachodzi: a stąd

^Fi ⁼^odśr>

_c M_z M_k _ M_k v r²    r

95