ssn1

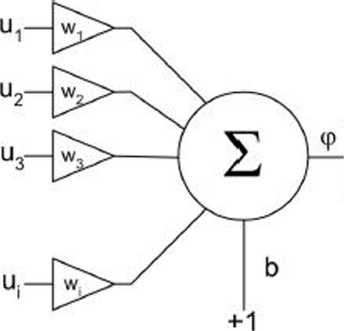
Model matematyczny neuronu

' m

y = F [<p\ = F Y, ^Wi • ^Ui + ⁶

,ł=0

y = F w^T • u 4- b

gdzie:

Ui - wejścia neuronu,

Wi - wagi neuronu (siły połączeń synaptycznych między neuronami), b- próg zadziałania neuronu (bias, parametr regulowany neuronu), y - wyjście neuronu.

F - funkcja wyjściowa.

i € (1.2,N) - indeks określający wejście neuronu,

N - liczba wejść neuronu.

Najczęściej stosowane funkcje wyjściowe

Sigmoida (krzywa logistyczna)	F (y?) - sgn (y?) - 1+^
Tangens hiperboliczny (tangensoida)	F (ip) = tgh (^1) =
Progowa (Heaviside'a)	F(V) = .	0    dla ip < 0 1    dla ip > 0
Liniowa	'n 2 II

Struktura ssn zależy od sposobu połączenia neuronów tej sieci oraz od kierunku przepływu sygnałów w sieci. Istnieje bardzo wiele rodzajów sieci neuronowych jednakże najbardziej popularne to

Sieci jednokierunkowe

Perceptron wielowarstwowy jest siecią w której neurony pogrupowane są w warstwy. Sieć tego typu posiada warstwę wejściową, wyjściową oraz jedną lub więcej warstw ukrytych. W warstwie wejściowej sygnały doprowadzone do sieci są wstępnie przetwarzane: normalizacja, filtracja lub skalowanie. Przetwarzanie neuronowe sygnału wejściowego odbywa się w warstwach ukrytych oraz w warstwie wyjściowej. Odpowiedź sieci neuronowej otrzymuje się na wyjściu neuronów warstwy wyjściowej a liczba tych odpowiedzi (sygnałów) proporcjonalna jest do liczby neuronów warstwy wyjściowej.

Sieci rekurencyjne

W sieciach tego typu występuje sprzężenie zwrotne między poszczególnymi warstwami. Oznacza to, że np. sygnały z wyjść podawane są na wejścia warstwy wejściowej lub ukrytej, co powoduje pewną dynamikę w pracy sieci. Sygnały wejściowe w takiej sieci zależą zarówno od aktualnego stanu wejścia jak i od sygnałów wyjściowych w poprzednim cyklu. Dużą użytecznością praktyczną cechują się sieci mające wszystkie połączenia o

charakterze sprzężeń zwrotnych. Sieci takie nazywane są sieciami Hopfielda (zastosov/anie m.in. jako pamięci asocjacyjne).

1

   sieci jednokierunkowe:

-    jednowarstwowe (perceptron prosty),

-    wielowarstwowe (perceptron wielowarstwowy),

•    sieci rekurencyjne:

-    lokalnie rekurencyjne globalnie jednokierunkowe (np. sieci neuronów dynamicznych),

-    globalnie rekurencyjne (np. sieci NARX, Jordana, Elmana),