str17

Przykład 14.10

Dana jest macierz kwadratowa stopnia drugiego

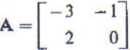
Funkcja    macierzy

i

f(A.) = e*‘ = £ oc,(OA* = <^(01 +a,(0A

k=0

równanie charakterystyczne macierzy A

g(2) => A³ + 32 + 2 ~ 0

stąd wartości własne macierzy

= — l; a₂ - -2

Na podstawie równań (14.234) przy n — 1

f(A₁) = e^>,' = e-' = a₀(?)-a_l(r) f(A₂) = e*^łl == e^_i' = a₀(i) —2a, (r)

a₀(ł) = 2e '-e'¹'

stąd

e

Af

Kj(i) = e e"^2<

= (2e^_<—e^-2')l +{e^-'

Ostatecznie wiec

' -e“' + 2e

—e~^z,)A =

2e^_t—2e

- Ir -21

e^-,+e~²' 1

2e^-1—e^-2r J

Metoda rozwinięcia w szereg skończony jest szczególnie przydatna wtedy, gdy macierz kwadratowa A ma wielokrotne wartości własne.

Niech macierz A ma m,.-krotną wartość własną A_;. Zależności (14.232) i (14.234) są nadal prawdziwe, lecz w celu obliczenia współczynników a₀(t),...,a_iLj(i) należy napisać dodatkowe równania w liczbie m^A— I uzyskane w wyniku obustronnego zróżniczkowania równania

fM = eV

df(A) d A

d²f(A)

dA²

X~ X:

(14.237) Piszemy zatem dodatkowe równania

2 «

= tc*^lt

X~Xt

dA

d²e^Af

dA²

= t²e^x‘‘

x=i:

A = A_f

d^m'-^,f(A)    d'"^i_ 1 e^At

dA^"¹    dA"¹'^-1

(14.238)

Przykład 14.11

Wyznaczymy funkcje macierzy e^A' dla '1 O O"

A= O 1    0.0 I 2. Równanie charakterystyczne

g(i) = det(AI-A) = (;.-2)(;.-l)(x-l) = 0

Wartość własna ł, = 2 jest jednokrotna, czyli m_t = I, a wartość własna i, = 1 jest dwukrotna, czyli m_z = 2. Przy n = 3 równanie (14.232) uzyska postać c^A’ = a₀(ł)l + a,(OA + a₃(()A²

W celu obliczania współczynników «(,{(), *i(0. *il') napifc^Aerny zgodnie z (14.234) i (14.238) równania

e^;,,^a₀(t) + a_t(OA₁+a₂(<)Af

= ^an(0+*i(0A₂+a₂(t)A₂

d _y ,,    d

■^-(e^ilł) = — [a_o(0 + «,(t)A₂ + a₄(t) Af]

<J/i₂    U/.2

te^v = a₁(/) + 2a₂(OA₂

a po podstawieniu A, = 2, ).₂ — li wykonaniu działań otrzymamy

17