00069 }db5d1dc19534077081f7b2f44fe560

68

Hembree & Zimmer

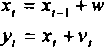
where w_t ~ N(0, a²w ) with unknown and v, ~ N(0, a\) with a\ known and w, v uncorrelated.

In order to use the DBAF, we have to find discrete prior probabilities across the rangę of a\ e (0, oo). It is not at all elear how these discrete points would be selected or how the prior probabilities would be assigned. We can look to the Kalman gain to get some insight to how this might be accomplished. Remember that for our model the Kalman gain converges to a steady State value of

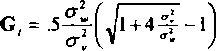
From the assumptions of this section, for any given Kalman gain value, a i is the only unknown. Therefore selecting discrete values across the gain is equiv-alent to discretizing across the unknown system error.

There are several advantages to discretizing across the gain. First of all, the gain only assumes values in the rangę (0, 1). This reduces the space of possible discrete values to a bounded rangę. Secondly, the gain provides intuitive direction for selecting values of system error and assigning prior probabilities. For instance, if the white noise contribution to error is Iow relative to the autocorrelation error, then the gain will tend toward 1.0. Likewise, if the expected autocorrelation in the data is Iow relative to the white noise contribution, the gain will tend toward zero. Usually these generał relationships are known and hence it should be relatively easy to assign informed prior probabilities to the discretely selected values of the Kalman gain.

Given the above arguments and assumptions, to construct the adaptive filter for this case, we must choose the k discrete values for the Kalman gain in the rangę (0,1) and construct k Kalman filters. We must also assign the initial prior probabilities to those k values of gain. Then, as illustrated in Figures 6 and 7, we input the measurement data to each of the k Kalman filters, calculate each of the k weighting functions and then take a weighted average as our estimate of the current process State.

The only part of this algorithm that has not been discussed in detail yet is the calculation of the function j\y_t 1% ,Ym )• Given our model assumptions,