FizykaII34101

335

335

mieniem AF. Linia prosta AR, pociągnięta z punktu A padania światła do punktu R rzeczonćj stycznćj, daje kierunek załamanego promienia, odpowiedniego padającemu promieniowi SA. Gdyż wystawiwszy w A prostopadłą PQ, będzie PAS kątem padania; żeby więc kąt RAQ był istotnie kątem załamania, a AR promieniem załamanym, musi proporcya:

sin SAP: sin RAQ — n\l.

mieć miejsce. Lecz tak jest rzeczywiście, bo w trójkątach ALK i ALR mamy

sin ALK: 1 — AK: AL, sin ALR : 1 — AR'. AL, zatćm sin ALK: sin ALR — AK: AR. Atoli kąt ALK—SAP, ALR — RAą, tudzież AK=AE, AR = AF, więc także sin SAP: sin RAQ = AL : AF. ^a Ponieważ na mocy wykreślenia

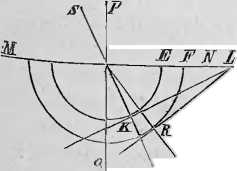
AL: AF = n: 1, zatćm ostatecznie sin SAP; sin RAQ — n:l, właśnie tak, jak twierdzono Dopóki n 1, zatćm AL y- AF (fig. 176), w którym to Wypadku załamanie do piouowćj ma miejsce, punkt L leży za-^Wsze za okręgiem koła, opisanego promieniem AF i konstrukcya ^ta dla każdego kąta padania daje się wykonać; jeżeli zaś ^AE < AF {Fig. 171), wówczas łatwo stać się może, że kąt padania SAP przekroczy pewną granicę wartości, dla któ-rćj L pomiędzy punkty L i F paść musi; w takim razie nie można już z L wykreślić stycznćj do koła, idącego przez punkt F.

Fin-, ni    Jest to omówiony wyżćj

_    przypadek całkowitego od-

mia. Mając przeciwnie do danego promienia załamanego wynaleźć odpowiedni promień padający, potrzeba tylko opisane, wylesienie wykonać odwrotnie, mianowicie najprzód wykreślić stycznę Rl do półokręgu, opisanego promieniem AF, potćm z L Poprowadzić stycznę LK do drugiego półokręgu i pociągnąć linię Prostą AK. Kierunek tćj ostatniej linii jest kierunkiem promienia padającego.