FizykaII03701

32

ści, posiadające różne znak’ położenia, według tego, czy

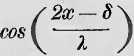
n —Ą-u, czy = — u. Wszystkie tedy punkta,

mające takie położenie, iż ten współczynnik = + w, znajdują się zawsze razem na jednćj stronie linii równowagi, te zaś, dla których on = — w, są zawsze razem na przeciwnćj stronie. Wszystkie tćż punk^Aa pojedynczych grup znajdują się razem w tśj s imćj fazie ruchu, punkta zaś różnych grup w fazach przeciwnych. Te pojedyncze grupy są od siebie pooddzielane punkta

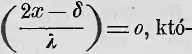
mi, dla których x ma taką wartość, iż cos

re przeto zostają ciągle w miejscu równowagi, jakąkolwiek wartość t przybierze. Cały szereg punktów rozpadnie się więc na pewną ilość części, z których każda zamknięta jest dwoma spo-czywającemi punktami, oddzielającemi ją od sąsiednićj. Punkta te nazwano węzłami, część zaś drgająca pomiędzy dwoma węzłami, nazywa się międzywęile. Wszystkie pojedyńcze punkta każdćj takićj części znajdują się razem w tćj samćj fazie, razem dosięgają kresu swćj dalekości drgania i razem powracają do swych miejsc równowagi, t. j. wykonują tak zwane stojące drgania, których czas trwania T równy jest czasowi, w jakim fala posuwa się dalćj o długość swoją. Dalekości więc drgania poje-dyńczych punktów są według wartości x rozmaite. Międzywę-źle zowie się tćż falą stojącą.

Dla dokładniejszego zbadania tych stojących drgań falowych przypuśćmy, że odległość S obu punktów, z których dwie fale wychodzą, jest i’ówna n ciorakićj ich długości, t. j.

S=z?i X; wówczas

/2x \    / t    n \

8= 2a cos I. -7 — ni u. sin 2r I ^---— J ,

r    2x    2x ~|

S—2a I cos n n. cos — a sin n h. sin — sr J .

r    t.    2nt    -|

\sin 2 ncos n Ti — cos — sin nti j .

czyli

zatćm

Lecz cos nr —±1, sin nn = o,

2x    t

8— 2a. cos — n. sin 2n —

(II.)