056

V nasledujicim prikladu tento vztałi zobecnime pro pravidclny n-uhelnik.

Priklad 6

V rovine je dan pravidelny n-uhelnik A₍₎AiA₂ ... A_n-i. Dokażte, ze pro każdy bod P teto roviny plati

|PA₀|² + \PA\|² + ... + \PA_n—i |² = n (R² + d²),

kde d je vzdalenost bodu P od stredu krużnice danemu n-uhelniku opsane a B je jeji polomer.

Reśeni

Protoże postup reśeni je stejny jako u prikladu predchoziho, mużeme postupovat. rychleji.

Pravidelny n-uhelnik A₀A\A₂ ... A_n-1 umistime v Gaussove rovine tak, aby body At, k = 0,1,2,..., n — 1, były obrazy komplexnich ćisel

( 2A/TI    2 /cti\

Xk = i? cos--f- i sin —- ), k = 0,1,2,... ,n — 1,

\ n    n )

coż jsou koreny binomicke rovnice xⁿ — Rⁿ = 0; komplexni cislo, jehoż obrazem je bod P, oznadime p. Plati pak

|PA₀|² + |PA₁|² + ... + |PA_n_₁|² =

= (P - jR)(p - R) + (p - xi)(p - x„_i) +

+ ... + (p-X_n-l)(p-Xi),

a protoże je pp = d², xix_n-i — x?x_n-2 = ... = x_n-\X\ = P², dosta-vame odtud

|PA₀|² + |PA₁|² + ... + |PA_n_₁|² =

= n (P² + d²) -p(R + xi + x₂ + ... + x_n_i) --p(R + x i +x₂ + ■■■ + x_n_i).

Protoże vśak plati

R + Xj + X2 + • • • + x_n~ i = 0,

A

|P.4₀|² + |PAi|² + ... + | PA_n-_X |² =n (R² + <t²), coź było zapotrebi dokazat.

Priklad 7

Urćete, ve kterem okamźiku je vzdalenost koncoveho bodu minuto-ve rućićky od koncoveho bodu rucieky hodinove rovna d, je-li delka minutove rućićky R a hodinove r.

Reśeni

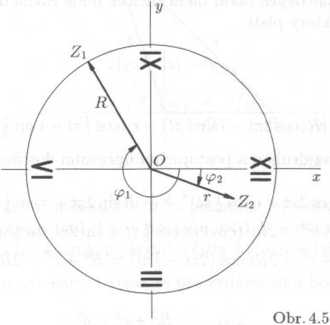
Mysleme si, że hodinove rućićky jsou umisteny y Gaussove rovine tak, że stred ciferniku je v jejim poćatku a ćislo dvanact na kladnć poloose realnych ćisel (viz obr. 4.5). Vyhoda tohoto umisteni (na prvni pohled ponekud neobvykleho, nebot’ dvanactka by mela byt spisę na ose ima-ginarni nad poćatkem) spoćiva v tom, że v okamźiku, kdy obe rućićky splyvaji s kladnou poloosou realnych ćisel a od ktereho budeme iriefit ćas, hodiny ukazuji 0 hodin. Ćas budeme merit. v hodinach.

111