060

Priklad 11

Dokaźte, źc pro koreny Xk, k = 0,1,2,..., n — 1 binomicke rovnice xⁿ — 1 = 0 a pro libovolne prirozene ćislo p plati:

a)    Je-li n delitelem ćisla p, pak

Xq +    + x% + ■.. + X^_j = Tl.

b)    Neni-li n delitelem ćisla p, pak x^Po + x[ + x£ + ... + <_! = 0.

Reśeni Jak vim

binomicke rovnice xⁿ -1=0 plati

, ,    ,    , „    2kn . . 2ku

Jak vime, pro koreny Xk = cos ---1- lsm-, k = 0,1.2,... ,n — 1,

n    n

2tc . . 2tc

Xo = 1, xi = cos--1-1 sm —

n    n

Xn—1 —

X2 = x\, X3 — xf,

Oznaćime-li s_P levou stranu dokazovanych rovnosti, plati

r^p

^cn-l ~

X2\P , (._r3\P ,    , Un-l\P

S_p = xg + X\ + Xl + . .. + x;_j =

= i+ *?+(*?)' +W)'+ ... + ₍«rT =

= l + s^p + x?^p + xf’ + ...+xlⁿ~^1)p.

Protoże jde o soućet prvnich n ćlenu geometricke posloupnosti s kvo-cientem xj, je nutno k jeho urćeni rozlisit dva pripady:

a)    Je-li x^p = 1, plati

s_p = 1 + x^p + Xj^P + xj^p +... + Xj^{! 1}^^p = l + l-l-l-(-l + ...-)-l^:=ri.

b)    Je-li x^p ^ 1, plati

Sp = 1 + x^p + xf + Xj^P + ... + x

(x^p)"-l (xD^P-l _n “ x^p-l ^_ x^p-l

nebot’ x? = 1.

Uvćdomime-li si. źe = cos--hisin-, je videt, źe pripad

2pn , . 2pn

n    n

n    n

Odtud dostayame, źe pripad x\ = \ na.st.ava pouze tehdy, plati-li

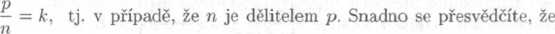
pripad rj ^ 1 nastaya jedine tehdy, neni-li n delitelem p. Tim je dane tvrzeni dokazano.

x^ — 1 nastayajedine pro cos = 1, tj. plati-li - 2kn, k 6 Z.

Vśimneme si jeSte zvlaśtniho pfipadu prave dokazane vety: Je-li p = 1, pak neexistuje żadne prirozene n > 1, ktere je delitelem ćisla p, także pro koreny binomicke rovnice xⁿ — 1 = 0 plati

#o + Xi + x-2 -t- ... + x_n-\ = 0.

Tento yysledek vśak uż zname: plati totiż pro każdou binomickou rov-nici.

K reSeni nasledujiciho (a posledniho) prikladu byste si asi kom-plexni ćisla nevybrali; v poślednim ze tri uvedenych zpusobu jeho re-śeni uvidite, że to je możne, a że to je dokonce velmi jednoduche a elegantni.

Priklad 12

Tri shodne ćtverce jsou urnisteny v rovine vedle sebe tak, jak ukazuje obr. 4.7. Urćete soućet yelikosti yyznaćenych uhlu a, (i, 7.

Reśent

H

E

G

F

B

C

D

Obr. 4.7

A

119