039

3.2 Binomicke rovnice

Biuomickou rovnici se nazyva rovnice tvaru

— a -

0,

kde a je dane kompłexni ćislo. x je neznama a n > 1 je ćislo pfirozene.

Nasuń ukolem je urćit vśechna komplexni ćisla. która teto rovnici vyhovuji. Mużeme pritom predpokladat. że je a ^ 0, nebot: je zrejme, ze pro a = 0 ma rovnice jedine reśeni, a to x = 0; tento pfedpoklad nain take umożni vyjadrłt ćislo a v goniometrickem tvaru.

Necht’ je tedy a = |a|(cos o + i sin a) a predpokladejme, źe ćislo x = |a:|(cosy! + i sin ę) je resenim dane binomicke rovnice, coź zname-na, źe pro nć plati

[|ar|(cosij? + isin^))] ” — |o|(cosa + i sin a) — 0; z Moivreovy vćty dostaneme

a:|ⁿ(cosny? + i sin rup) = |a|(cosa + i sina).

Jak vime, z rovnosti dvou ćisel v goniometrickem tvaru plyne, źe se rovnaji jejich absolutni hodnoty a argumenty se lisi o cely nasobek ćisla 2it (także se mohou i rovnat, je-li tento nasobek nulovy); odtud plyne

|zr|"'= |a|, rup = a 4- 2kn, k e Z.

Pro ćisla |x|, <p tak dostavame

1*1 =

a + 2 ku n

k € Z,

także

x = v/jo| (cos

/ a + 2fer:

n

+ i sin -

a + 2kn

n

ke Z.

O tom, ze nalezena ćisla x jsou opravdu resenim dane binomicke rov-nice, se snadno presvćdćite jejich dosazenim do teto rovnice.

Na prvni pohled by se mohlo zdat, źe techto ćisel je nekonećne mnoho, nebot’ k probiha nekonećnou mnożinu v§ech celych ćisel. Avśak vzhledem k periodicite funkci sinus a kosinus tomu tak neni: k tomu, abychom dostali vśechny ruzne koreny binomicke rovnice xⁿ — a = 0, staći dosadit za k pouze ćisla 0, 1, 2, ..., n — 1. Ukaźme si pro ilus-traci, źe pro k — n dostaneme toteż ćislo jako pro k — 0:

a + 2- O- rr .. a + 2- 0- 7t --h i sin-

cos

n

n

)

Shrneme:

Binomicka rovnice

xⁿ - |a|(cos a + i sin a) = 0

ma v oboru komplexnich ćisel pravć n ruznych korenu, a to

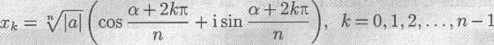
77