051

1

noboli

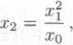
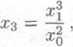
%n— 1

2 *

Pro soućet korenu dane binomicke rovnice tak dostavame

#0 + #i + #2 + ®3 + • • • + %_n—i —

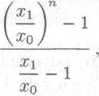
x\    x\    x? ¹

-^o+^H---i—o    • • • d—rió    —

Xo    £q    ^0

nebot’ jde o soućet prvnich n ćlenu geometricke posloupnosti s prv-

nim ćlenem xq a s kvocientcm — / 1 (viz poznamka na str. 29).

Xq

Uvedomime-li si vsak, źe

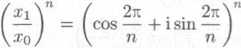
cos 2ti + i sin 2rc

1,

dostavame

£0 + X\ + X‘2 + • • • + X_n-1 = 0,

coz znamena, ze soućet vśech navzajem ruznych korenu binomicke rov-nice je roven nule.

S temito dvema vetami dokaźeme v nasledujici śestici prikladu za-jimave vztahy, ktere plati pro nektere pravidelne n-uhelniky. V poślednich Sesti ulohach vystaćime pak jen s tim, co było vyloźeno v prvnich trech kapitolach teto ućebnice. Ukazuji moźnosti vyuźiti komplexnich ćisel ke studiu rovnomernćho pohybu po kruźnici, k dukazu sinove a kosinove vćty, k odvozeni nćkterych vlastnosti kombinaćnich ćisel apod. Uvedenymi typy uloh vśak moźnosti pouźiti komplexnich ćisel nejsou ani zdaleka vyćerpany; velmi zname je jejich vyuźiti ke studiu elektrickych obvodu se stridavym proudem.

Dokażte, że velikost strany pravidelneho devitiuhelniku je rovna roz-dilu velikosti jeho nejdelśi a nejkratśi uhloprićky.

Reśeni

;

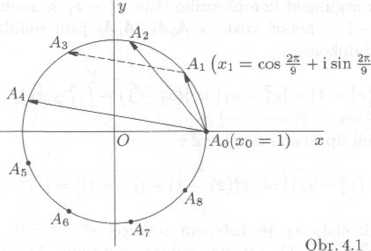
Oznaćime vrcholy pravidelneho devitiuhelniku .4o, Ai, .4g a bez ujmy na obecnosti budeme predpokladat, że je vepsan do jednotkove krużnice v Gaussove rovine tak, że każdy z vrcholu Ak, k — 0,1,... ,8, jc obrazem cisi a

2kn . . 2ku    .

z* =cos—+ ism—,    & = 0,1,...,8,

ktere je korenem binomicke rovnice — 1 = 0 (viz obr.4.1). Velikost strany daneho devitiuhelniku jc |.4₀/li|, velikost jeho nejkratśi, resp. nejdelśi uhlopricky je |i4oj4₂|, resp. |4.₀4₄|. Marne dokazat, że plati

|^4o^4.4I ~ |^4o^4.2I — |^4o-4i|-

Pri dukazu postupne upravime levou stranu dokazovane rovnosti, nej-prve takto:

|^4o--4-4 | — |;4oj42 I = |    — 11 — |    — 11

101