0657

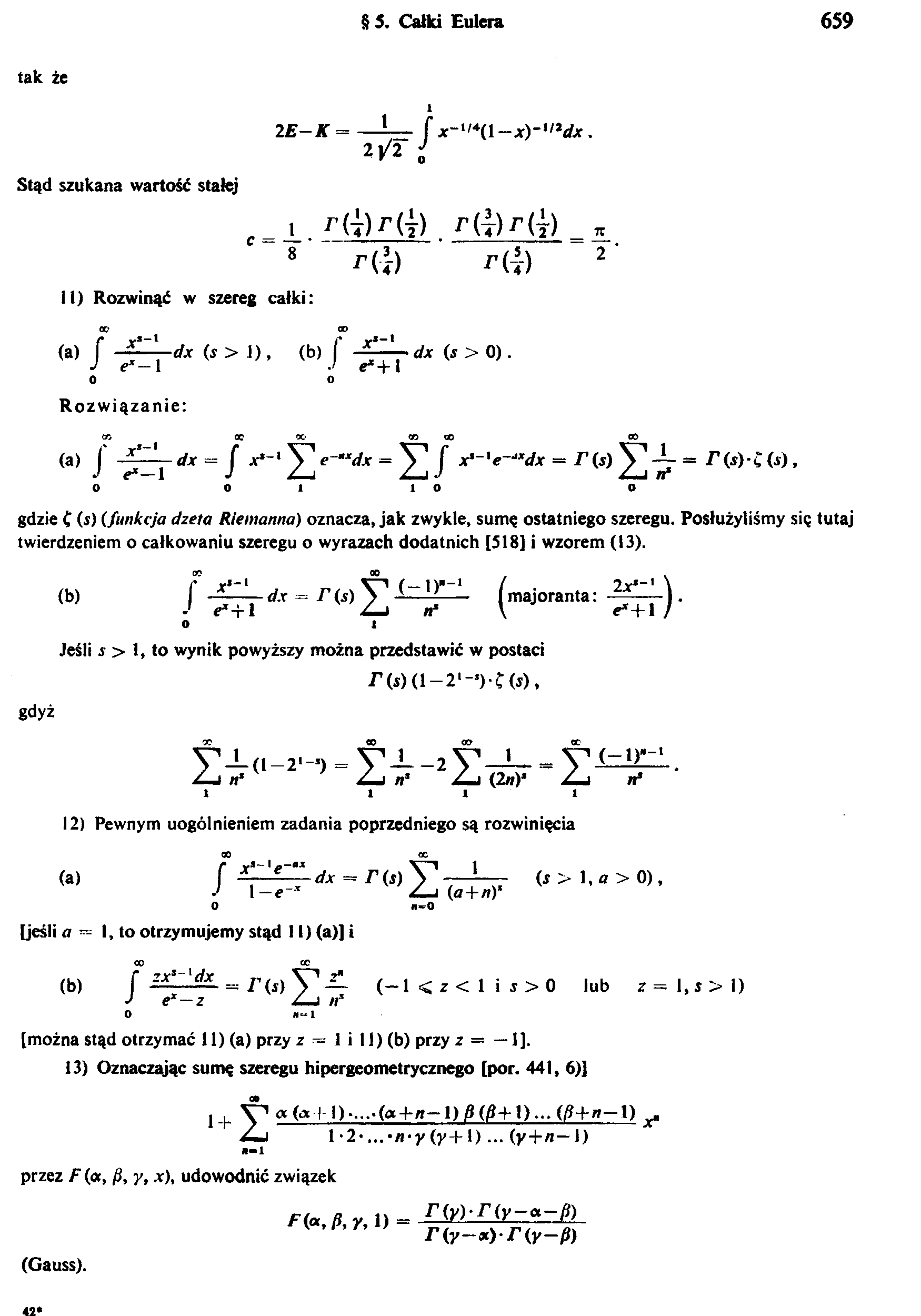
tak że

§ 5. Całki Eulera

659

1

2E—K

2\/2 ^J

Stąd szukana wartość stałej

c = — 8

1    tt

r{\)

r$)

II) Rozwinąć w szereg całki:

OD    00

(a) f -r-r^dx <* > D -    (^b> f -zrrr^dx c* > o> ■

J e^x— 1    •' e*+l

o    o

Rozwiązanie:

Oł    00    00    00 CO    CO

(a) j -p—— dx — J x^s~‘ 'y ^ e~^xxdx =    * J x*~'e~"dx — r(s) ^ * — = Z¹ (i)■ C U) ,

o    oi    i o    o

gdzie C (i) (funkcja dzeta Riemanna) oznacza, jak zwykle, sumą ostatniego szeregu. Posłużyliśmy się tutaj twierdzeniem o całkowaniu szeregu o wyrazach dodatnich [518] i wzorem (13).

^(b)    J i^^dr = ^r(s)£^1:iP^L (^majoranta:-Srr)-

O    1

Jeśli s > 1, to wynik powyższy można przedstawić w postaci

r(«)(l-2^,-)-C(ł),

gdyż

CC    00    CO    OC

y -L(i-2'-‘) = y j__₂y _±_ = y

Z_i n-    Z_i n* Z_j (2#i)*    n*

12) Pewnym uogólnieniem zadania poprzedniego są rozwinięcia

(a)

f ^x-~'^e “ dx = T(s) V-!- (s > 1, a > 0),

J \-e~^x    4Li(a + ny [jeśli a ~ I, to otrzymujemy stąd 11) (a)] i

CO    OC

(b) f ZślTlŚL ₌ r (s) y —    (— 1 < z < 1 i j>0 lub Z=1,J>1)

J e^x—z    i »^s

O    a-l

[można stąd otrzymać 11) (a) przy z = 1 i 11) (b) przy z = — 1].

13) Oznaczając sumę szeregu hipergeometrycznego [por. 441, 6)]

1 +

I

H-l

<* (■> + !)•■ 1-2

(<x+n-l)0(P+\)...(fl+n-l) ^ ■ ■•n-y(y+ I)... (y+n-1)

przez Z (<x, /S, y, x), udowodnić związek

F{«, /?, y, 1) =

r(y)-r(y-ot-p) r{y-<x)-r{y-p)

(Gauss).