0668

670

XIV. Całki zależne od parametru

Widać stąd od razu, że znak /'(u) dla —n<a< —(n— 1) jest taki sam, jak znak czynnika (— 1)¹. Gdy a dąży do —n lub do — (»— 1) (tzn. gdy a dąży do zera lub do 1), to jT(a) dąży do <x> (pierwszego rządu!)

9)    Korzystając z zadania 8) uogólnić wzory (7), (9), (15), (20), (26), (30) na przypadek dowolnych rzeczywistych wartości argumentu (z wyjątkiem wartości całkowitych ujemnych oraz zera).

Wskazówka. Przy uogólnianiu wzoru (30) należy wziąć pod uwagą wzór (33).

Przy uogólnieniu r (a) na przypadek ujemnych wartości a wzór Gaussa, o którym była mowa w za¹ daniu 7), pozostanie prawdziwy przy jedynym zastrzeżeniu, ze y—x—fi> 0. Jest ono konieczne dla zbieżności szeregu F(«, fi, y, 1) [378, 4].

10)    Wychodząc z wzoru (34) udowodnić, że jeśli ¹ przebiega od 0 do 1, to /"(a—n) raz tylko przechodzi przez wartość 0 zmieniając przy tym znak z (— 1)"^+I na (—1)¹. Oznaczmy tą wartość a przez <¹,. Dla wartości a, równej a,—n, funkcja r (a) ma zatem minimum dodatnie, (gdy n jest parzyste) lub maksimum ujemne (gdy n jest nieparzyste). Porównaj wykres funkcji r na rysunku 64 (str. 648).

Proponujemy również udowodnić, że przy rosnącym n zarówno «„ jak i T, = lF(a_M—n)l maleją monofonicznie do 0.

Wskazówka. Należy tutaj oprzeć się na następujących równościach (0<ot<l):

|r («-(»+1))| =

Jf-t-1—(X

|r(¹-(n+i))r

ir(»->,)r . ir(«—«)i

M+l-a    (/I+l-«)² oraz

r'(«.)    y I

r(¹.)    Z_i v-<x„ ‘

»-i

11) Udowodnić, że przy —n<a< —(n— t) funkcja F(a) wyraża się całką

r{d) =

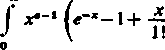
*•-¹ («—!)!

)

dic.

Wskazówka. Całkować przez części; patrz 8).

12) W rozdziale XI [402, 10)] zdefiniowaliśmy funkcję r (a) za pomocą wzoru Eulera-Gaussa (7) dla dowolnych rzeczywistych wartości argumentu (z wyjątkiem zera i wartości całkowitych ujemnych) i posługując się tą definicją znaleźliśmy niektóre najprostsze własności tej funkcji [por. też 408]. Podobnie można znaleźć również i inne własności.

Innym punktem wyjścia dla zbadania funkcji r (a) dla dowolnych rzeczywistych wartości argumentu (z tymi samymi wyjątkami) może być szereg

H-.0

z dodatkowymi warunkami .T(l) = Z¹ (2) = 1.

13) Zaznaczmy jeszcze na zakończenie, że funkcja r (a) może być określona również jako jedno-wartościowa funkcja analityczna na całej płaszczyźnie zmiennej zespolonej a (')• Można to zrobić wychodząc z definicji całkowej (6), jeżeli się rozbije całkę na dwie

f + f =P(a) + <2(o).

o t

1

Ta uwaga o rozszerzaniu funkcji F będzie zrozumiała jedynie dla czytelników zaznąjomionych z podstawowymi pojęciami i terminami teorii funkcji zmiennej zespolonej.