0566

568

XIV. Całki zależne od parametru

Na przykład, nie oblicząjąc całek

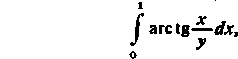
J In (x²+y²)dx,

O

widzimy od razu, że są one ciągłymi funkcjami parametru y dla dowolnych dodatnich jego wartości.

507. Różniczkowanie pod znakiem całki. Przy badaniu własności funkcji (1), która określona jest za pomocą całki zawierającej parametr y, zasadnicze znaczenie ma problem istnienia pochodnej tej funkcji względem parametru.

Przy założeniu istnienia pochodnej cząstkowej f_y(x, y) Leibniz podał regułę obliczania pochodnej którą w oznaczeniach Lagrange’a można napisać tak:

»

(10)    = fnu<y)dx lub posługując się wymowniejszymi oznaczeniami Cauchy’ego:

b    b

D_y f/(x, y) dx = f D,f(x, y) dx .

a    a

Jeżeli takie przestawienie symbolu pochodnej względem y i całki względem x jest dopuszczalne, to mówimy, że funkcję (1) można różniczkować względem parametru y pod znakiem całki.

Taki sposób obliczania pochodnej będziemy nazywali regułą Leibniza.

Następujące twierdzenie podaje proste warunki wystarczające na to, aby można było stosować tę regułę.

Twierdzenie 3. Niech funkcjaf (x, y) określona w prostokącie (a, b\c,dj będzie ciągła względem x w przedziale <«, bj przy dowolnie ustalonym y z przedziału <c, d). Załóżmy dalej, że w całym prostokącie istnieje pochodna cząstkowa f(x, y), ciągła jako funkcja dwu zmiennych (¹). Wówczas przy dowolnym y z przedziału (c, </> prawdziwy jest wzór (10).

Ciągłość funkcji f{x,y) względem x gwarantuje istnienie całki (1).

Ustalmy dowolnie wartość y = y₀ i weźmy pewien przyrost tej zmiennej Ay — k.

Jest zatem

»    b

I (y₀) = / f(x, y_Q) dx,    I (y₀+k) = J f(x, y₀+k) dx ,

a więc (U)

Hy₀+k)-I(y₀) ₌ f f(x, y₀+k)-f(x,y₀) ^

k    J    k

1

Z tych założeń wynika już ciągłość funkcji /(.r, y) względem obu argumentów, nie będziemy jednak z niej korzystali.