1132

Zdefiniowane wcześniej mierniki pozwalają odpowiedzieć na następujące pytania:

•    o ile min egzemplarzy zmienił się nakład książek i broszur w kolejnych latach w porównaniu z rokiem poprzednim lub z rokiem 1995 (^,,,995);

•    o ile procent zmienił się nakład książek i broszur w kolejnych latach w porównaniu z rokiem poprzednim (d_ŁT_, • 100) lub rokiem 1995 (d_WS95 ■ 100);

•    jaki procent nakładu książek i broszur z danego roku stanowi nakład z roku następnego (4m • 100) lub jaki procent nakładu z roku 1995 stanowi nakład z kolejnych lat (foflM* 100)-

Pozostawiamy czytelnikowi do interpretacji poszczególne wartości liczbowe z tabl. 7.8.

7.4. PRZELICZANIE INDEKSÓW

Czasem istnieje potrzeba wyrażenia dynamiki w ujęciu łańcuchowym, podczas gdy dysponujemy jedynie indeksami o stałej podstawie. Może też zdarzyć się odwrotna sytuacja, że analizując w długim okresie zmiany pewnego zjawiska chcemy je przedstawić za pomocą indeksów jednopodstawowych, a posiadamy informacje wyłącznie o indeksach łańcuchowych. Indeksy są miarami, które łatwo dają się przekształcać.

Załóżmy, żc mamy informacje o dynamice pewnego zjawiska w postaci indeksów o stałej podstawie z pierwszego okresu. Zapiszemy je zgodnie z definicją tej miary następująco:

(7.9)

Żeby otrzymać indeksy łańcuchowe wystarczy podzielić dwa indeksy o stałej podstawie z sąsiednich okresów; przy czym indeks i_m jest jednocześnie indeksem łańcuchowymi dla drugiego okresu.

Zgodnie z definicją indeksu łańcuchowego dla okresu trzeciego mamy:

(7.10)

(7.11)

*3/2    •    ‘3/1 * *2/1

*2 *! *.

W w-ersji ogólnej, dla dowolnego okresu / otrzymamy:

•    — ^X' —    • ^X,~^l — i

*1/1-1 — —    ■ ~ • »,_!/!

1    -*1

W tym przekształceniu indeksów¹ wykonujemy takie samo działanie jak wówczas, gdy indeks liczymy z definicji dzieląc przez siebie dw^rie wielkości absolutne.

Nieco trudniejsze są przekształcenia w sytuacji, gdy wyjściowymi informacjami sa indeksy łańcuchowe, a chcemy jc przekształcić w wersję jednopodstawową. Mamy wówczas:

. x₂ .    *,    .    _ x,

*2/1 —    >*J/2 ^—    (7.12)

*1    ^X2    ^XK-l

Tak jak poprzednio indeks i_2n jest jednocześnie indeksem łańcuchowym oraz indeksem o podstawie z pierwszego okresu. Kolejne indeksy jednopodstawowe będziemy wyznaczać następująco:

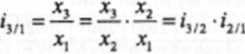
X_A    X₄ X, x₂    .

^!vi ^{—    —}    ~^l4/i‘h/2‘^l2n

X,    X, x₂ X,

(7.13)

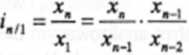
—— •_— — i • i'    .    . •    . i

•" *3/2 *2/1

Jak widać w formule (7.13) indeks jednopodstawowy dla dowolnego okresu t będzie iloczynem indeksów łańcuchowych dla okresu i oraz wszystkich wcześniejszych.

Przykład 7.8.

W tabl. 7.9. źródłowymi są dane o dynamice liczby pracujących (wersja łańcuchowa). Indeksy o podstawie z roku 1992 zostały obłiczone zgodnie z formułą 7.13. Pamiętać należy, źe przekształcenia dotyczą wartości indeksów zgodnie z ich definicją, natomiast w tablicy każdy indeks jest wyrażony w procentach (mnożony przez 100). Przy wykonywaniu przekształceń trzeba go zatem przez 100 podzielić, a dopiero ostateczny wynik zamienić na procenty.

Tablica 7.9. Dynamika liczby pracujących w gospodarce narodowej

Rodzaj indeksu	1993	1994	1995	1996	1997	1998	1999	2000	2001	2002	2003
Rok poprzedni = 100	97.6	101,0	101,8	101,9	102.8	102,3	97,3	97.7	99,4	85,3	99,9
Rok 1992= 100	97.6	98,6	100.4	102,3	105,1	107,5	104,6	102,2	101,6	86,7	86,6

Źródło: indeksy łańcuchowe Rocznik Statystyczny Przemysłu 2003. s.XXXVI-XXXVII, tabl. I, Ip. 1, indeksy jednopodstawowe - obliczenia własne oraz www.stat.gov.pl.

Każdy rodzaj indeksu pokazuje nieco inny obraz zmienności w czasie liczby pracujących. W latach 1994-1998 mamy do czynienia ze wzrostami tej kategorii, od 1% (tempo wzrostu) w stosunku do roku poprzedniego w pierwszym roku, do 2,3% w ostatnim. Potem następuje spadek i dotyczy on wszystkich kolejnych lat. Najbardziej dotkliwym jest spadek liczby pracujących w roku 2002, bo jest on rzędu 14,7%. W porównaniu z niewielkimi spadkami z lat 1999-2001, to gwałtowna zmiana. Ze względu na opisaną na podstawie dynamiki łańcucho-

203