1134

obserwujemy wielkości absolutne zjawiska, przy czym wystarczy posiadać informacje o wielkości zjawiska w pierwszym i ostatnim okresie analizowanego przedziału czasowego. Jeśli podstawimy do wzom 7.15 zamiast każdego indeksu iloraz wielkości absolutnych zgodnie z definicją indeksu 7.5, to otrzymamy po zredukowaniu odpowiednich wyrażeń:

*"o

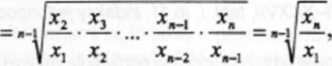
(7.17)

ponieważ w pierwszym ułamku licznik redukuje się z mianownikiem drugiego, w drugim licznik jest tą samą wartością, co w mianowniku ułamka trzeciego itd. Pozostaje mianownik pierwszego i licznik ostatniego ułamka.

Przykład 7.11.

Wróćmy do przykładu z liczbą absolwentów szkół dla dorosłych (por. tabl. 7.7). Licząc średni indeks przy użyciu średniej geometrycznej mamy:

I_G = VU04 • 1,105 1,1 • 1,087 • 1,094 • 1,015 - 0,997 = iJWS (7.18)

W Excelu wystarczy skorzystać z funkcji Średnia.Geometryczna.

Problem obliczenia pierwiastka siódmego stopnia można rozwiązać wykorzystując przekształcenie logarytmiczne oraz fakt, że pierwiastek jest potęgąo wykładniku równym odwrotności jego stopnia (1/7). Zatem mamy:

i_e =(1,615)'’    (7.19)

Po zlogarytmowaniu stronami wyrażenia (7.19) otrzymamy:

, /? \ ln(l,615) 0,47933 _rtA.₀_

ln(i_c)= ■’ =    = 0,0685    (7.20)

Prawa strona wyrażenia jest liczbą, którą można obliczyć przy użyciu kalkulatora. Można też sięgnąć po funkcje arkusza Excel: Potęga (dla obliczenia 7.19), Ln (do formuły 7.20) lub Exp (przy wyznaczaniu 7.21). Funkcji tych należy szukać wśród funkcji matematycznych. Ostatecznie wyznaczamy średni indeks używając funkcji odwrotnej do logarytmownia:

~i₀ = cxp(0,0685)= 1,0709    (7.21)

Średnioroczne tempo wzrostu liczby absolwentów szkół dla dorosłych w okresie 1995-2002 wynosi 7,09%, gdyż:

f = 1,0709 100-100% = 7,09%    (7.22)

7.6. INDEKSY AGREGATOWE

Indeksy agregatowe są miarami dynamiki, które stosuje się do kategorii będących niejednorodnym agregatem, składającym się z różnych składników'. Najczęściej indeksy te liczone są w celu wyodrębnienia ze zmian w- czasie wartości pewnego agregatu wpływu zmian ilościowych oraz zmian cen.

Jeżeli dokonujemy zakupu pojedynczego artykułu (np. bułki na śniadanie) w większej ilości, to wartość tego zakupu będzie iloczynem ilości i ceny jednostkowej tego artykułu:

w=qp    (7.23)

gdzie:

w - wartość zakupionych bułek (w zł), q - ilość zakupionych bułek (w sztukach), p - cena jednej bułki (w zł za 1 sztukę).

Równanie 7.23 przedstawia relację między trzema kategoriami: wartością, ilością i ceną. Zakupu takiego dokonujemy w różnych okresach i dla każdego okresu relacja 7.23 jest spełniona, przy czym każda z kategorii, która w niej występuje może kształtować się na odmiennym poziomic. Dla każdej z tych kategorii możemy też określić miarę dynamiki, w szczególności indeksy indywidualne. Załóżmy, że porównujemy dwa okresy: wcześniejszy, oznaczony symbolem „O" oraz późniejszy, dla którego przyjmiemy symbol „1”. Zdefiniujemy indeksy indywidualne ilości, wartości i ceny w następujący sposób:

w,    Qi    . Pt

t_w =—, i =— oraz / =—    (7.24)

^W0    Po

gdzie:

i_w - indeks wartości, i_q - indeks ilości, i_p - indeks ceny.

Można wykazać, że pomiędzy trzema indeksami określonymi przez formułę 7.24 zachodzi taka sama zależność, jak między wielkościami absolutnymi 7.23, czyli żc indeks wartości jest iloczynem indeksu ilości i indeksu ceny:

(7.25)

Powyższa zależność nazywana jest równością indeksową.

Rozważmy teraz sytuację, gdy dokonujemy zakupów różnych artykułów. Każdy z nich może być wyrażony w odmiennych jednostkach miary. Będzie nas interesować agregat składający się z k artykułów. Wartość tego agregatu będzie sumą wartości każdego z artykułów, a ta z kolei iloczynem ilości i ceny:

W = ±qj'P„    (7-26)

t-1

gdzie W oznacza wartość agregatowego zakupu, a symbol ; jest numerem artykułu. Zatem q, jest ilością zakupionego artykułu j, apj jego ceną. Wartość agrega-

207