1139

•    tendencja rozwojowa - czyli trend,

•    wahania okresowe (sezonowe),

•    wahania koniunkturalne,

•    wahania przypadkowe.

Tendencja rozwojowa ujawnia się poprzez systematyczne jednokierunkowe zmiany (wzrost lub spadek) poziomu badanego zjawiska, zachodzące w długim okresie. Charakter tych zmian (systematyczność i długotrwałość) pozwala przypuszczać, iż przyczyną występowania określonego trendu w rozwoju zjawiska jest stałe oddziaływanie na zjawisko pewnego splotu czynników' - przyczyn głównych.

Wahaniami okresowymi nazywamy rytmiczne wahania o określonym cyklu (okresie przebiegu). Najczęściej obserwmjc się w^rahania o cyklu rocznym, przy czym podokresami cyklu w takim przypadku mogą być półrocza, kwartały, miesiące, czy nawet dni.

Wahania koniunkturalne to systemowa, falowe wahania rozw-oju gospodarki, obserwowane w dłuższych od roku okresach.

8.1. WYKRYWANIE GŁÓWNEJ TENDENCJI ROZWOJOWEJ

Rozwoźmy przypadek szeregu czasowego, w którym możemy obserwować dość systematyczne zmiany w czasie (trend) oraz towarzyszące im zmiany przypadkowa. Rysunek 8.1 przedstawia liczbę samochodów osobowych w' Polsce w latach 1995-2002.

Wykres 8.1. Przykład rosnącej tendencji rozwojowej zjawiska

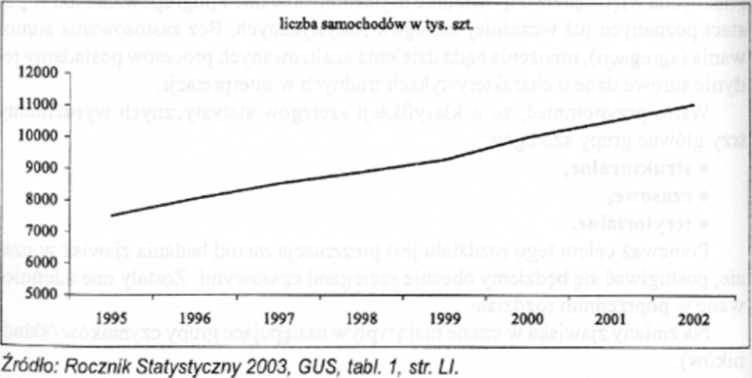
W przypadku prezentowanego zjawiska czyli liczby samochodów Y będzie miała zastosowanie liniowa funkcja trendu zapisana w postaci:

(8.1)

y,=b_rt + b₀.

gdzie:

y - teoretyczne wartości Y wyliczone z funkcji trendu,

b_x - współczynnik funkcji trendu (współczynnik kierunkowy funkcji),

b₀ - wyraz wolny,

/ - jest zmienną wyrażającą czas o wartościach definiowanych zazwyczaj zgodnie z numeracją kolejnych okresów, dla których dysponujemy informacjami (t = 1. 2.... n).

Funkcja (8.1) jest szczególnym przypadkiem ogólnej linii regresji (6.5), gdzie oznaczenie zostało zastąpione przez t.

Funkcja liniowa ma stały kierunek rozwoju danego zjawiska i jest on wyznaczony przez współczynnik kierunkowy prostej W funkcji trendu (8.1), parametr ten jest współczynnikiem stałego przyrostu wartości zmiennej prognozowanej w ciągu jednostki czasu.

Metodą szacowania parametrów funkcji liniowych jest klasyczna metoda najmniejszych kwadratów (jak pokazano w rozdziale 6). Parametr)' funkcji trendu można obliczyć na podstawie następujących formuł:

M    IV

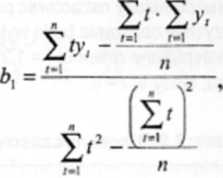
(8.2)

(8.3)

K=y-*> i'\

gdzie:

±y.    1<

y =    .    i=*~,    (8.4.)

n    n

n - liczba badanych okresów.

Na podstawie powyższych wzorów wyznaczamy parametry 6, i b₀. dzięki czemu ostatecznie możemy uzyskać postać szukanej funkcji trendu.

217