162

A HibUl. IM1U.1 .Vvu    r ), buui :uO

ISBN D4H1II S-7. © l>. WN TOS >*}

162

5 SYMETRIA CZĄSTEC2EK

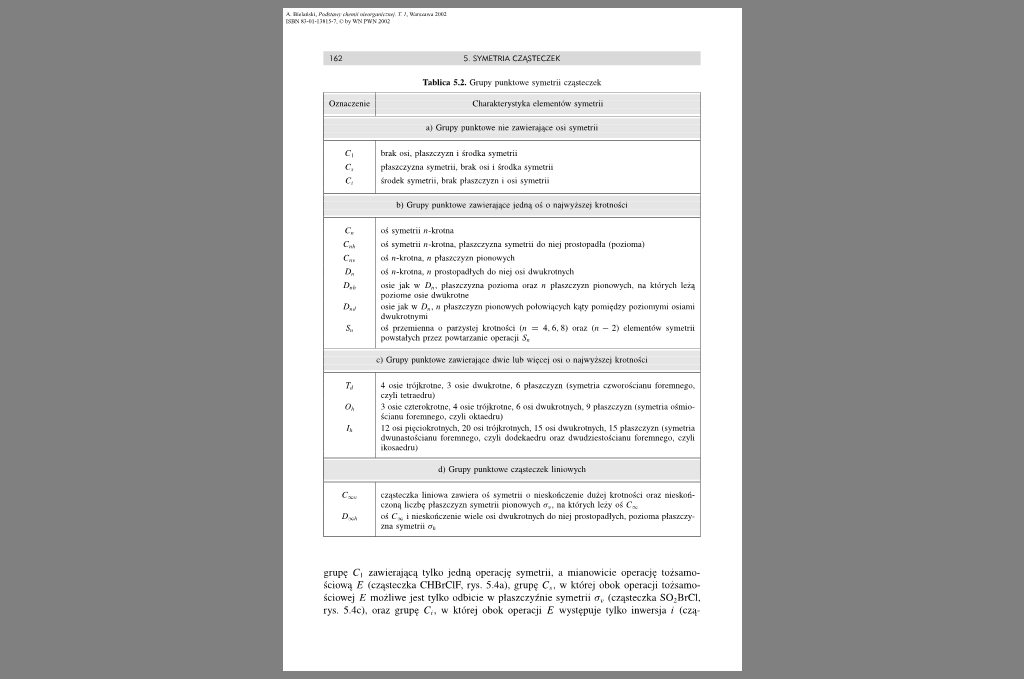
Tablica 5.2. Grapy punktowe symetrii cząsteczek

Oznaczenie	Charakterystyk* elementów symetrii
aj Grupy punktowe nie zawierane osi symetrii
c,	brak osi. płaszczyzn i środka symetrii
C,	płaszczyzna symetrii, brak osi i środka symetrii
c,	środek symetrii, brak płaszczyzn i om symetrii
b) Grapy punktów zaw waiące tedrti oś o najwyższej krotności
c.	oś symetrii rt-kriAna
O	oś symetni n krittiu. płaszczyzna symetrii do mej prostopadła ipoziomai
c.	uś n-krotna. n płaszczyzn pionowych
n„	oś n-krotna.« prostopadłych do niej osi dwukrotnych
o.r	osie jak w E)„. płaszczyzna pozioma oraz n płaszczyzn pionowych, na których leżą poziome osie dwtikratne
O.z	osie jak w l),. n płaszczyzn pionowych połowiących kąty pomiędzy poziomymi osiami dwukrotnymi
s.,	oś przemienna o parzystej krotności (;i = 4.6. 8> oraz (n - 2) elementów symetrii powstałych przez powtarzanie operacji 5,
O Grupy punktowe zawierające dwie lub więcci osi o n.iiwyzszci kiotności
T,	4 osie trójkrotne, ś osie dwukrotne. 6 płaszczyzn (symetria czworościanu foremnego, czyli tetraedru)
Os	y osie czteiokrutne. 4 osie trójkrotne, 6 osi dwukrotnych. 9 płaszczyzn (symetria ośnuo-ścianu foremnego, czyli oktaedruj
h	12 osi pięciokrotnych. 20 osi liójkrotnych, 15 osi dwukrotnych. 15 płaszczyzn (symetna dwunastościnnu foremnego, czyli dodekaedru oraz dw-udzicttościanu foremnego, czyli
	ikosaedru)
dl Grapy punktowe- cząsteczek liniowycli
	cząsteczka liniowa zawiera oś symetrii o nieskończenie dużej krotności otaz nieskończoną liczbę płaszczyzn symetrii pionowych <r,. n* których leży oś Cx
	oś C\ i nieskończenie wiele osi dwukrotnych do mej prostopadłych, pozioma płaszczyzna symetrii

grupę C'i zawierającą tylko jedną operację symetrii, a mianowicie operację tożsamościową F. (cząsteczka CHBrCIF, rys. $.4a), grupę C,, w której obok operacji tożsamościowej E możliwe jest tylko odbicie w płaszczyźnie symetrii a,, (cząsteczka SO.BrCl. rys. 5 4c). oraz grupę C,. w której obok operacji E występuje tylko inwersja > (czą