226

A HibUl. IM1U.1 .Vvu    r ), buui :uO

ISBN D4H1II t-7. © by »N TOS >*}

226

7 CIAŁO STAŁE

Energię sieciową. t/₀, odniesioną do 1 mola cząsteczek substancji można obliczyć

^ZWZoru    NA<h. u

V_n =

dltfoTo

^Ł(-i)

(7.2)

wyprowadzonego przy uwzględnieniu oddziaływań elektrostatycznych pomiędzy wszystkimi jonami dodatnimi i ujemnymi tworzącymi sieć przestrzenną. Wzór uwzględnia fakt, ze w przypadku małych odległości pomiędzy jonami zaczynają odgrywać coraz większą rolę siły odpychania także i pomiędzy jonami przeciwnego znaku, wynikające z nakla dania się na siebie powłok elektronowych obu jonów. Przy małych odległościach siły te wzrastają bardzo gwałtownie, w miarę jak sąsiadujące atomy przybliżają się do siebie.

We wzorze (7.2) jY oznacza liczbę Avogadra, e — ładunek elektronu. Z- i — liczbę elementarnych ładunków ujemnych anionu i dodatnich kationu. *■« — przenikał-ność elektryczną próżni, r<, — odległość dwóch sąsiednich jonów przeciwnego znaku. n — współczynnik wyznaczany na podstawie badań ściśliwości kryształów, przyjmujący dla jonów o konfiguracji elektronowej helu wartość 5. dla jonów o konfiguracji neonu wartość 7. dla jonów o konfigurac ji argonu wartość 9. dla jonów o konfigurac ji kry ptonu wartość 10 i o konfiguracji ksenonu wartość 12. Stała A we wzorze (7.2) nosi nazwę stałej Madelunga i zależy od sposobu ułożenia jonów dodatnich i ujemnych w sieci przestrzennej Dla struktur typu NaCI przyjmuje ona wartość 1.7476. dla struktur typu CsCI — wartość 1.7627, dla siiuktur typu CaF_; — wartość 5.0388-

Energię sieciową można także obliczyć z pew nych danych doświadczalnych na podstawie cyklu Borna i Habera, opisywanego szczegółowo w podręcznikach chemii fizycznej

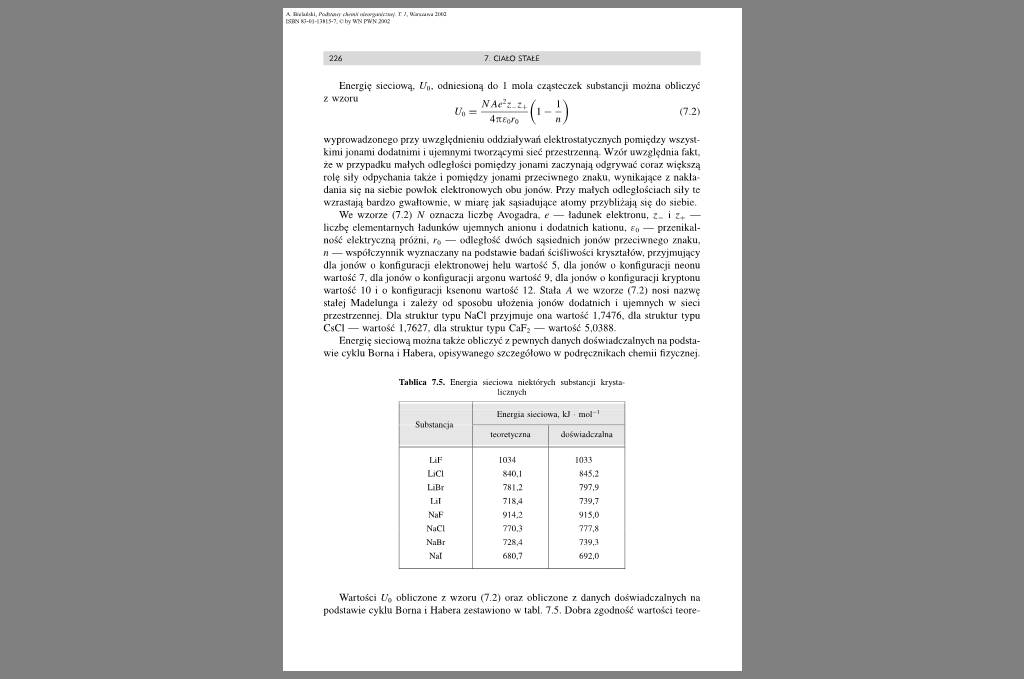
Tablica 7.5. Encryia nccicm-a niektórych substancji kryita licznych

Substancja	l.nm'i.1 sieciowa, U mol ^1
	teoretyczna	doświadczalna
lal-'	1034	1033
LiCI	840.1	845.2
laBr	781.2	797.9
Li!	718.4	739.7
NaF	914.2	915.0
NaCI	770.3	777.8
NaBr	728.4	739.3
Nal	680.7	692.0

Wartości Ł'₀ obliczone z wzoru (7.2) oraz obliczone z danych doświadczalnych na podstawie cyklu Borna i Habera zestawiono w taki. 7.5. Dobra zgodność wartości teore