179

A HibUl. IM1U.1 ,Vvu    r ), buui :uO

ISBN D4H1II ł-7. © by »N TOS >*}

5 4 CHARAKTERY REPREZENTACJI GRUP SYMETRII    179

Obydwu operacjom C* i C.4 odpowiadają różne macierze, ale o takich samych wartościach charakteru. Podobne związki istnieją pomiędzy operacjami symetrii polegającymi na odbiciu w płaszczyźnie v- i w płaszczyźnie yz Obydwie operacje przedstawia się za pomocą dwóch niejednakowych macierzy, wykazujących jednak takie sanie charaktery. Odpowiednio do tego w nagłówku kolumny piszemy zamiast a,, i a,, tylko symbol 2tr,. To samo można powiedzieć o dwóch operacjach o,,.

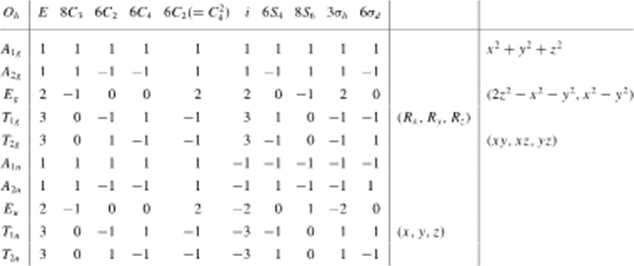
W poprzednim paragrafie rozważaliśmy przekształcenia składowych x. y. z wektora OP (rys. 5 14) pod wpływem operacji symetrii grapy Cu i stwierdziliśmy, że wektor z przekształca się według reprezentacji A,, czyli stanowi bazę tej reprezentacji. Stwierdziliśmy także, te wektory x i y stanowią bazę reprezentacji dwuwymiarowej /: Wnioski takie zostały odnotowane w trzeciej kolumnie tablicy charakterów grupy Ca,, przez podanie symboli z lub (,v. y). W analogu do tego mozenty odczytać z tablicy charakterów grupy C,< że wektor x, a także wektor y stanowią bazy jednowymiarowej reprezentacji A', wektor z natomiast bazę reprezentacji 4“. W grupie 7,. wektory x. y. z stanowią wspólnie bazę trójwymiarowej reprezentacji 7V Omówienie symboli R,, R-,. R. ozna czających obroty wokół osi ,t. y i c możemy tutaj pominąć.

Kolumna czwarta tablicy określa właściwości transformacyjne kwadratów oraz iloczynów dwuczynnikowych współrzędnych x, y. Z- 7. tablicy grupy C₄, wynika więc. ze oraz suma x² + y² stanowią bazę reprezentacji /ł|. różnica v^:    y* bazę reprezentacji

Bi, iloczyn xy bazę reprezentacji R_:, a iloczyny xz oraz yz. wspólnie bazę reprezentacji dwuwymiarowej E.

Informacje zawarte w kolumnach trzeciej 1 czwartej są ważne, gdyż na ich podsta wic wnioskujemy o właściwościach transformacyjnych orbitali atomowych. Właściwości transformacyjne orbitali p_K, p, i p są bowiem takie same, jak właściwości transformacyjne wektorów x, y i z; właściwości transformacyjne orbitali r/,_y, d_x! i takie same. jak iloczynów xy. xz 1 yz: właściwości transformacyjne orbitali 1 </,• _v- wreszcie są takie same. jak kwadratu z² i różnicy kwadratów x^z - y². Możemy to sprawdzić rozważając transformacje orbitali tl_:: 1 według operacji grupy C_4l . Posłużymy się przy tym rys 3.14 przedstawiającym kształt tych orbitali.