s2 zad14 s1

Drgania własne symetrycznej ramy portalowej

(S) Na rys. 8.9S,Sa,Sb został pokazany zastępczy schemat dla symetrii o LSSDW = 2, z dwiema masami drgającymi mi = m/2 i n»2 = m, a także wykresy momentów jV/-^S' wywołane jednostkowymi siłami Pj^S^ = 1 [ ], dla i = 1,2. Aby uprościć obliczenia przemieszczeń Sij dla schematu połówkowego RSP-S (o SSN = 1 i SKN = 1), rysujemy dodatkowo wykresy momentów    (w statycznie wyznaczałnych ramach), uwzględniając je we

wzorze Maxwella-Mohra

Au =

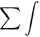
MiM[

El

d.s- =

1.847 El '

M₂m, ~eT^As

0.444 El '

Aia = Ć21 — y

ds = -

m\m₂

El

0.440 El ’

Szczegółowe obliczenia, związane z rozwiązaniem problemu własnego, prowadzą do następujących wyników:

(4^S), A⁽!^S) = (A„, A₂₁}^(s) ) = (0.964y^ , Ar = (-2.879,+1.000}), (^u2    = {A]2, A₂₂}^ ) = ( 1.852 J— , A₂ = (+0.695, +1.000} ).

(A) W drugiej części zadania chcemy opisać antysymetryczne postacie drgań (rys. 8.9A,Aa,Ab). Rama o zastępczym schemacie połówkowym o LSSDW = 2 jest statycznie wyznaczalna, stąd łatwość sporządzenia wykresów momentów m\ , dla i = 1,2. Na podstawie przemieszczeń

M₂M₂ ,    5.75

“ET^d,= £7'

c    f M\M\ 14.0

^{dll =} ^J^r^ds = -eT'

ai₂ — A21 =

M1M ₂ El

ds =

8.68

El

budujemy równanie problemu własnego, którego rozwiązaniem są następujące dwie pary:

(o>5^a,,A⁽₁^a) = (Au, A₂₁}^(a) ) = (0.282y— , Al = (+1.566,+1.000} ), (U^A>,a!,^A> = (A₁₂,A₂₂}^(A)) = (2.206^/^, A, = (-1.278,+1.000} ).

Na rys. 8.9el-e4 zestawiono cztery formy drgań własnych analizowanej ramy portalowej, w kolejności wynikającej z uporządkowanego widma częstości drgań

.,<^s)

.,in —,(s)

,iv

= OJ

(A) 2 ■

Najniższa częstość drgań, zwana podstawową, jest związana z najprostszą postacią antysymetryczną.