82455

Część 2    15. DRGANIA WŁASNE RAM - OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5

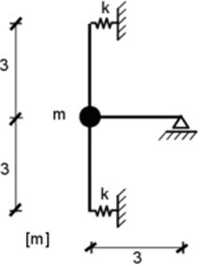
Rys. 15.5. Rama obciąiona masą skupioną Parainetiy geometryczne i fizyczne układu są następujące:

EJ = 31000 kNm*

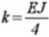
m = 200kg

Masa ma możliwość ruchu w dwóch kierunkach (SSD = 2). icli kierunki i siły dynamiczne będące wynikiem działania bezwładności masy przedstawiono na rys. 15.6.

3

/

3

/

[m]

r'*i

w,. B,

i

vil|

B, = -mw,(t) B. = -mWj(t)

Rys 15.6. Układ obciążony dynamicznie

Funkcja rozwiązująca różniczkowe równanie ruchu dla digaii harmonicznych ma postać:

w_ł(/)=a_l sin w i fr, (/)=-«,«>■ sinwt

(15.8)

Wiemy, że na przemieszczenie w danym kierunku wpływ mają obie siły:

[ir₂{t)=6_2lB,+6₂₂B_:

Po podstawieniu wyrażeń na siły bezwładności otrzymujemy układ równali różniczkowych:

(15.9)

Dobra D.. Dziakicwlcz L, Jainbrożrk S.. Koniora M.. Mikołajczak E.. Przybylska P.. Sysak A.. Wdowska A.

AlmaMater