starosol4

176

3. Stropy płytowo-belkowe

F

3.3. Obliczanie

177

Przyjmując, że można aproksymować idealnie sztywność zastępczą jako funkcję m₀, mentu maksymalnego dla tego schematu, stwierdzono, że samo przejście na odmienny schemat obciążenia pociąga za sobą błąd przeszacowania ugięcia w granicach 5-t40%. W przypadku obciążeń równomiernych błąd ten jest niewielki — nie przekracza na ogól 5%. Oczywiście powyższe wyniki otrzymano dla określonej konkretnej sytuacji.

Przedstawione wyżej modele dotyczą najczęściej obciążeń debiutujących (pierwsze obciążenie narastające od zera do wartości M_u) lub obciążeń o niewielkiej liczbie powtórzeń. Z praktycznego punktu widzenia istotny jest model pracy przekroju pod obciążeniami długotrwały mi. Jest to zagadnienie bardzo aktualne, ale dalekie od rozwiązania. Technicznie rozwiązywane jest ono przez:

•    odpowiednią zmianę wartości E_s i E_c, co występuje m.in. w metodzie Muraszewa,

•    odpowiednie mnożniki zwiększające wynikowe ugięcia obliczane dla obciążeń doraźnych,

•    dodatkowe mnożniki zwiększające ugięcia doraźne od wpływu pełzania i niezależne dodanie wartości ugięcia od wpływu skurczu.

znacznym przeszacowaniem ugięcia w przypadku obciążenia przęsła jedną siłą skupioną lub obciążeniem odcinkowo ciągłym.

Innym przyjęciem rozkładu sztywności jest sposób syntetycznie pokazany na rys. 3.67b, gdzie w obszarze poza rysami uważa się, że przekrój pracuje jako niezary-sowany, a w miejscach występowania rys mamy do czynienia z dodatkowymi sprężystymi obrotami (Borcz) lub strefą o skończonej długości, w której sztywność określa się jak dla fazy II (Ryżyński, Apanas).

Założenie kontynualnej zmiany sztywności np. według wzorów (3.78), (3.79) (Kuczyński) prowadzi przy zastosowaniu lej zasady na całej długości pręta do wykresu zmian sztywności, przedstawionego na rys. 3.67c. Jedynym zastrzeżeniem, które można wnosić do tego rozkładu, jest brak w strefie minimalnych momentów odcinka o stałej sztywności. Jednakże w przypadku „mutacji y/’ (por. rys. 3.65h) zarzut ten praktycznie ma znaczenie jedynie formalne.

3.3.7.2. Ugięcia i redystrybucja momentów

TE.

Punktem wyjścia w określeniu ugięć zbrojonych elementów betonowych zginanych zarówno izo-, jak i hiperstatycznych jest ogólnie znana zależność między krzywizną,

momentem zginającym i sztywnością giętną:

m	_ d^2y	_	(3.80)	a) _ _	. - ../i!!lir!^1
UJ	dr XI	B . ’ XI			i

w której (l/p)_x/, M_xi, B_xi są odpowiednio: krzywizną, momentem i sztywnością w przekroju x od obciążema o i-tej intensywności.

Wyrażenie (3.80) pozwala po dwukrotnym scałkowaniu otrzymać ogólny wzór do określania ugięcia

y =    d*dy + C_xx + C₂.    (3.81)

Aby rozwiązać zagadnienie, i to zarówno dla elementu statycznie wyznaczalnego, jak i ciągłego, jest konieczna znajomość prawa rządzącego wartością B_xi na całym obszarze całkowania. W elementach ciągłych dodatkowym utrudnieniem jest fakt, że przebieg momentów zginających M_xi zależy od rozkładu wartości B_xi na długości elementu.

Uprzednio omówiliśmy zagadnienia przebiegu funkcji (M, 1/p) dla pojedynczego przekroju, co jest równoznaczne z określeniem dla takiego przekroju funkcji moment-sztywność (M, B). Tutaj omówimy jedynie rozkłady tych funkcji na długości elementu, dla uproszczenia statycznie wyznaczalnego (rys. 3.67).

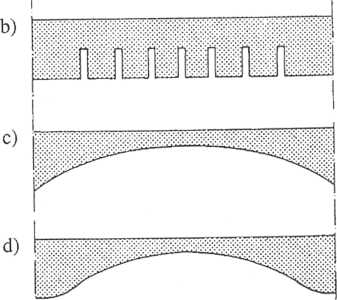
Bardzo często, jak już o tym wspominano, przyjmuje się stałą sztywność zastępczą na długości jednoimiennej gałęzi wykresu momentów (rys. 3.67a). Jest to ujęcie najprostsze, najczęściej stosowane także w normowych sposobach obliczeniowych, ale grożące

Rys. 3.67. Zmienność sztywności belki żelbetowej (B) na długości przęsła (opis w tekście)

Konsekwentne uwzględnienie na długości elementu uzyskanego z pomiarów wykresu pracy przekroju (por. rys. 3.65i) prowadzi do wykresu zmienności sztywności, przedstawionego na rys. 3.67d. Można go także uzyskać przy różnych modelach pracy przekroju. Dla porównania na rys. 3.68 [177] przedstawiono konkretne wartości funkcji sztywności w zależności od sposobu przyłożenia obciążenia i jego intensywności.