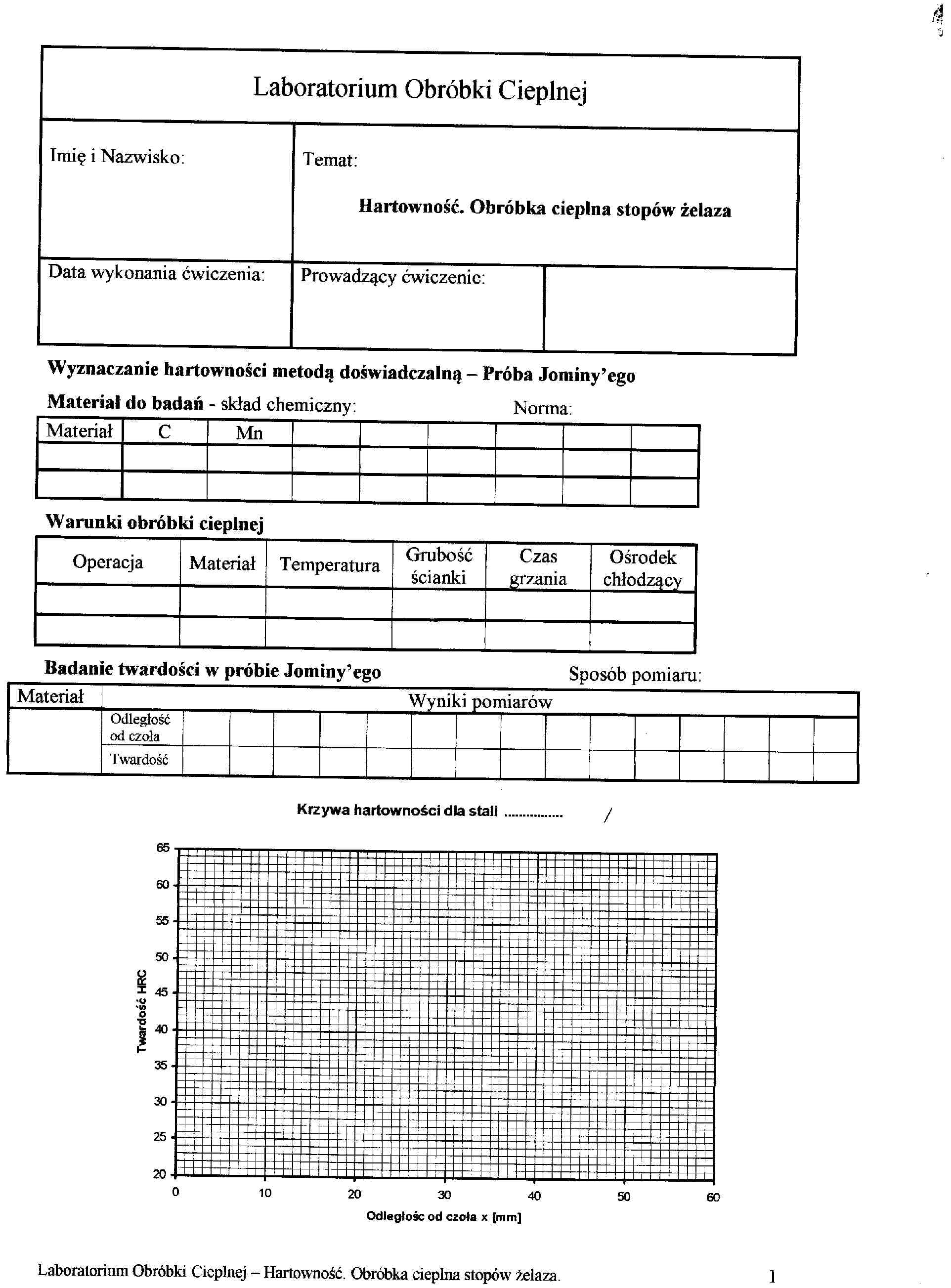
img152 (4)

3. Rozwinięcie w szereg trygonometryczny.doc, 7/16

ROZWINIĘCIE SYGNAŁÓW W SZEREG WYKŁADNICZY FOURIERA (cd)

dotychczasowe rozważania dotyczyły przedstawienia dowolnego sygnału x(t) za pomocą szeregu w przedziale skończonym (r₀,/₀ + T)

poza tym przedziałem sygnał x(r) oraz odpowiadający mu szereg Fouriera, nie muszą być sobie równe

jeśli sygnał x(t) jest okresowy, to można wykazać, że jego rozwinięcie w szereg dotyczy przedziału nieskończonego (-qo,oo)

dowód

rozważmy sygnał x(r) oraz jego rozwinięcie w wykładniczy szereg Fouriera w przedziale

(toJo + T)

x(t)=

i=-<x>

równość ta jest spełniona w przedziale {t_Qit₀ + T), poza tym przedziałem niekoniecznie prawa strona równania jest okresowa (o okresie T ), gdyż

_eJi®o(<+^T) _ejMot_eP<**T _ o‘ 3. Rozwinięcie w szereg trygonometryczny.doc, 8/16

ROZWINIĘCIE SYGNAŁÓW W SZEREG WYKŁADNICZY FOURIERA (cd)

zatem jeśli sygnał x(t) jest okresowy z okresem T to równość (rozwinięcie w szereg) jest zachowana w przedziale nieskończonym (-00,00), czyli