str213

EGO § 2. KLASYFIKACJA RÓWNAŃ LINIOWYCH Z DWIŚMA ZMIENNYMI 213

ące równanie różniczkowe:

0.

pu danego równania ;cnie równanie różniczkowe

V

cterystyk:

chodzimy do nowych zmien-

ównaniu otrzymanym z rów-

⁵A

ty

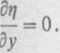
:ępującą postać kanoniczną:

•islamy również w zależności

Zadanie 2.5. Sprowadzić do postaci kanonicznej równanie różniczkowe:

₄3²m    „ , d²u _d²u _du

W

9y^ł~z~~2 by²t x h26= 0.

^    * dx² ' dxdy ' dy²t dy

Rozwiązanie. Obliczamy 5 dla określenia typu danego równania (2)    5 =-B²—AAG = 36/-72/ = -36/.

Równanie (1) jest zatem typu eliptycznego. Piszemy obecnie równanie różniczkowe charakterystyk

^9/(s)⁺⁶//²-⁰’

skąd mamy

(3)

dy _ -l±i

dx~ 3/ '

Rozwiązaniem równania (3) jest następująca rodzina charakterystyk:

x+y³±ix = C.

Dla sprowadzenia równania (1) do postaci kanonicznej przechodzimy do nowych zmiennych £ i r\ (2.15) określonych następującymi zależnościami:

(4)    £ = *+/, t] = x.

Obecnie obliczamy współczynniki występujące w równaniu kanonicznym

^A‘ ‘ ^C‘    ~^A{£) ^+ł£'I^+C(l)²"    - 9/.

B, =0,

|lf_+ii^_+c£!f₊4«₊4₌₆^-_W = i₈/.

dx² 8xdy dy² dx dy

d²t\ _nd²r\ ^d²r\ dtj _Ł drj

b_l — A—4 + B—~- +C—j+a -—\-b — = 0. dx² dxoy dy² dx dy

We współrzędnych ć, i t] równanie (1) przybiera następującą postać:

fd²u d²u\ du

<⁵>    %⁺a?j-²3{-⁰-

Końcową postać zależności (5) otrzymujemy po wyznaczeniu y = y/^-rj ze związków (4) i podstawieniu do zależności (5). Jest to równanie