str221

§ 2. KLASYFIKACJA RÓWNAŃ LINIOWYCH Z DWIEMA ZMIENNYMI 221

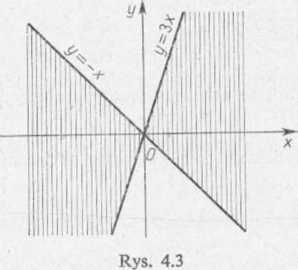
c)    część półpłaszczyzny ograniczona prostymi y = — x i y — 3x, tzn. dla x<0 jest 3x<y< — x oraz dla x>0 jest —x<y<3x, część zakreskowana na rysunku 4.3,

d)    punkty leżące na zewnątrz elipsy —+y²>l.

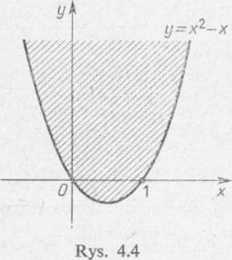
2. a) Wnętrze paraboli y>x²—x, część zakreskowana na rysunku 4.4,

b)    dla półpłaszczyzn y< — 3x—2 lub y> — 3x+2,

c)    w półpłaszczyźnie y> — $(x+1),

d)    w paśmie —2<x<2.

.    du\

^sm~*r\dż⁺W~ ’

d²u ¹

3- a) 12—— H-sin dtfti

,. d²u d²u ^b) dę²+d_n²~^0,

4. u(x, y) = F(co s 2x+2.v+y) + G (cos 2x — 2x+y).

§ 3. Równanie Laplace’a

Definicja 1. Równaniem Laplace'a nazywamy następujące równanie różniczkowe

cząstkowe:

(3.1)    _V²u = 0, gdzie y²u jest laplasjanem funkcji u

(3.2)    y²u = div(grad u).

W zależności od rodzaju układu współrzędnych laplasjan (3.2) przybiera odpowiednią postać:

a) we współrzędnych prostokątnych (kartezjańskich) x, y, z