img257

HIPERBOLA Definicje, oznaczenia

Hiperbola jest zbiorem wszystkich punktów X płaszczyzny, które są oddalone od dwóch wzajemnie różnych punktów £, F o stałą bezwzględną wartość różnicy ich odległości 0<2a<|£F| . Wtedy prawdziwe jest: ||FAj - \EX\\ = 2a.

Oznaczenia: E,F - ogniska, S - środek, .1. B - główne wierzchołki,

a długość głównej osi biegunowej, b długość sąsiedniej osi

biegunowej, e mimośrodowa (mimośrodkowość) e = | FSj = \ja² + b²

Równanie hiperboli

Rów nanie osiow e

X² V²

S[0;0], EFa_X\    =

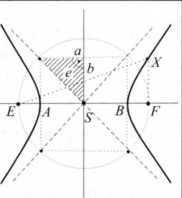
S[m;n], £F||x: (* ^mY _ (V ⁿ? ₌ ] a²    b²

x² v²

£[0;0], EFay:

b² a²

S[m\n\, EF\\y\    = 1

b²    a²

Rów nanie ogólne:

£F||x: Ax² -By² + Cx +Dy + E = 0, gdzie zl>0. B>0, EF\\y: -Ax² +By² + Cx+Dy + E = 0, gdzie A>0, B>0.

Równanie parametryczne:

a

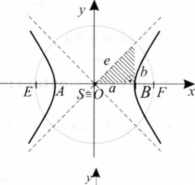
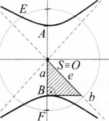
S[0;0], £Fcx: x

cos^>

y = btg<p, gdzie 0°s^<360°, tp* 90°,270°, a> 0, b> 0,

S[m;n], EF\\x: x = m +-, y = n + blg<p. gdzie 0°i^<360°, <p*90°,270°, a>0, b>0.

cos tp

Analogicznie dla innych pozycji stożkowych.

Obszar leżący wewnątrz i na zewnątrz hiperboli

EKTORY I GEOMETRIA ANALITYCZNA

I