img137 (2)

6. Analiza korelacyjna.doc, 5/19

PODSTAWY ANALIZY KORELACYJNEJ (cd)

możemy napisać

1 00 1 »

(x,y) =— Jy(co)x(“a>)da) = — jY (ca )X*(($)dcQ 2n    2 te

—co    —co

powyższą zależność nazywamy uogólnionym wzorem Rayleigha, z którego wynika, że iloczyn skalarny dwóch sygnałów jest proporcjonalny do iloczynu skalarnego ich widm

powyższy wzór można zapisać w postaci wyrażenia podcałkowe w powyższych wzorach w ogólnym przypadku są zespolone, natomiast lewe strony z założenia są rzeczywiste

wykorzystując parzystość części rzeczywistej i nieparzystość części urojonej widma sygnału rzeczywistego możemy napisać

X{- m)Y'(- co) = X'(<»)y(<o)=

6. Analiza korelacyjna.doc, 6/19

PODSTAWY ANALIZY KORELACYJNEJ (cd)

oraz wykorzystując ogólną zależność

Z + Z* = 2ReZ

możemy wprowadzić funkcję rzeczywistą postaci

^R4^x(®)^y'(^co)]

przy użyciu której iloczyn skalamy sygnałów x(f) i y(t) można przedstawić w postaci

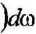
— 00

funkcja O_xy(co) nazywana jest widmem energii wzajemnej sygnałów x(/) i

powyższa postać iloczynu skalarnego wyraża strukturę wzajemnych powiązań (korelacji) między dwoma sygnałami, wynika z niej, że w formowaniu energii wzajemnej sygnałów różne zakresy ich widma odgrywają niejednakową rolę, największy wkład zapewniają te przedziały częstotliwości, w których widma sygnałów pokrywają się