skanuj0004 (414)

66 Rozdział J. Ciągi i szeregi

zatem 8_n —> O, czyli ś/a — 1 + ó_n —» 1. Jeśli O < a < 1, to a = J, gdzie b > 0, ^a v^/5=^5-⁺I = ¹-

Analogicznie można udowodnić równość (4.9). Zauważmy, że {/n > 1, gdy n > 1. Zatem yfn = 1 + e_n, gdzie e_n > 0. Ze wzoru Newtona mamy:

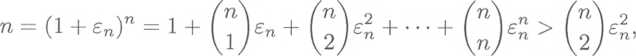
czyli n > ^ n{n — l)e^, zatem 0 < e_n < yj. Stosując ponownie twierdzenie o trzech ciągach (twierdzenie 4.21), otrzymujemy e_n —> 0, czyli y/n —> 1.    □

Przykład 4.32. Obliczmy granicę ciągu a_n = y/7ⁿ + 8ⁿ + 10ⁿ. Zauważmy, że zachodzi następująca nierówność:

10ⁿ ^ 7ⁿ + 8ⁿ + 10ⁿ sC 10ⁿ + 10ⁿ + 10ⁿ = 3 • 10ⁿ.

Zatem

10 - a/KP sC (/7M^ \/3 • 10ⁿ sC ^3-10.

Ponieważ \/3 —> 1, więc skrajne ciągi są zbieżne do 10. Jeżeli zastosujemy

jeszcze raz twierdzenie o trzech ciągach, widzimy że ciąg a_n = y/7ⁿ + 8ⁿ + 10ⁿ jest zbieżny do 10.

4.2. Szeregi liczbowe

Niech będzie dany ciąg (a_n)£2__l5a_n G M. Dla dowolnej liczby naturalnej N rozważmy sumę:

N

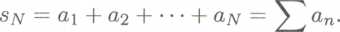
n=l

Precyzyjną, indukcyjną definicję powyższej sumy przedstawiono w przykładzie 3.15. Ciąg (s/v) nazywamy ciągiem sum częściowych.

Definicja 4.33. Formalną sumę nieskończoną

oo

OO

(4.10)

N

nazywamy szeregiem. Szereg a_n nazywamy zbieżnym, jeśli ciąg s/v =    ^an

n= 1

jest zbieżny (tzn. zbieżny do pewnej liczby rzeczywistej s), gdy N —» oo. Wtedy

oo

piszemy s — ]T) a_n.