14175 skanuj0018 (182)

80

Rozdział 4- Ciągi i szeregi

4.12. a_n = 4n — \/l6n² + 6n — 5. 14.13. a_n = V4n² + 5ra - 7 - 2n."

v 4.14. a_n = \/n² — 1 — n.^rQ

__ /V

i 4.15. a_n — y/n² — n + 1 — n.— " V?

„ 4.16. a_n — \Ai⁴ + n² — y/n^Ą — n².

4.38.    a_n

4.39.    a_n

4.40.    a_n

4.41.    a_n

= arcsin (\/n + 1 - y/n).

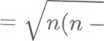
Vn² - 1).

- O*²)". = (i-ir-

4.17.    a_n

4.18.    a_n

4.19.    a_n

4.20.    a_n

4.21.    a_n

= V 3 n² + 2n — 5 — n\/3. = Vn² — 2n — \Zn² + 2 n. = \/ 4n² + n — 2\Jn² — 1. = y/n + ^/n - \Jn- sfn.

__ _n_

\Ai²+l+\/27i² + l "

4.22.    a_n

4.23.    (i_n

2 n—1

\/n²+l+n ‘ \/n²4-5—n

\ZP+2-n'

4.42.    _a„ = (tl)²".

4.43.    o, = (1 - 2)²"

4.44.    «„=(!_ X)⁴"

4.45.    a_n = (2±S)²’*.

4.46.    a„ = (1 + i)²"

4.47.    a„ = (1 -

4.59.    a,

4.60.    a_r

4.61.    a_r

4.62.    a_n

4.63.    a_n

4.64.    a_n

4.65.    a_n

4.66.    a_n

4.24. a_n = '4.25. a_n =

4.26.    a_n =

4.27.    a_n =

4.28.    a_n -

4.29.    a_n =

4.30.    a_n =

4.31.    a_n =

4.32.    a_n =

4.33.    a_n =

4.34.    a_n =

4.35.    —

4.36.    a_n —

4.37.    a_n =

n—3

\/n²+n—\/n²+2

• A

\/9n²4-3n+l —3n"

3n² — -\/n³ +1 — n² —2n+4 '

^n³ + n — n.

ś^n³ + 2n² — n.

V^n³ + 2n — 1 — n.

\/n³ + 5 — n.

n(\/n³ + n — n).

4.48.    a„ = (^)”².

4.49.    o„ = (1 + 2)⁴ⁿ.

4.50.    a_n =

4.51.    a„ = (l - -Z,)²"³.

⁴-⁵²- =

4.53. a„ = (n±l)²”.

\/n³ — n — (n — 2).

^71^ + 277 — 71 n

\Zn³ —71+1—n 71 — 1

_71+1_

\Z9n³—3n+l—3n

5n_

\/8n³+n—n

1

\/8n³+5n—2n

4.54.

4.55.

4.56.

4.57.

4.58.

^71 —	^n+2j^n+!
a 71 ^=	0 “ ^	r
a 71 ^=	(*+	2 71
a 71 ^:	f n^3 )	7i^2—5n
<2/1 ~ |	(n^2+2\ i 71^2—2 )	n 2

4.67.    a_n

4.68.    a_n

4.69.    a_n

4.70.    a_n

4.71.    a_n

4.72.    a_n

4.73.    a_n

4.74.    a_n

4.75.    a_n

4.76.    a_n

4.77.    a_n

4.78.    a_n

4.79.    a_n