Image47 (15)

181 Rozwiązania zadań ze zbioru "MENDLA "

_{Wi =} P5_^b._(Ta__Tb)

Pb * Vb

Wartość ^c-=-wyznaczymy z równania Clapeyrona dla stanu B.

Tb

PB • Vb Tb

= n ■ R

T_b = 200K

i    Ta = 300K

(300K-200K)

Wi = 1 mol• 8,31

Po podstawieniu do Wi mamy: Wi = n • R • (Ta-Tb) J

K ■ mol

Wi = 831 J

Podczas przemiany B-C objętość gazu jest stała, więc praca W2=0.

W czasie trzeciej przemiany C-D gaz wykonuje pracę rozprężając się izobary-cznie, skąd mamy:

W3 = - p • AV , ale AV = Vd - Vc, więc W3 = - po • (Vd - Vc)

Z równania przemiany izobarycznej wyznaczymy Vc Vc V_D . _

Tc ⁼ Td ^/TC

V₀ =

Vp • Tc Td ^_

Po podstawieniu Vc do pracy W3 możemy obliczyć jej wartość. W3 = - po • I Vd -    ^"^C

W3 = po

W3 = pd

Td

Vd - Tc .. ^ ⁷ V_d-Tc V_d-T_d^

Td

Td

W₃ =    • (Tc - T_D)

= n • R

Z równania Clapeyrona dla stanu D otrzymamy PD • Vp Td

skąd W3 = n • R • (Tc - Td)

W₃= 1 mol• 8,31

(100AC— 300K)

J

K ■ mol

W₃ = - 1662 J

Całkowita praca wykonana przez gaz podczas całego cyklu wynosi:

W = W1 + W₂ + W₃ W = 831 J+ 0- 1622 J W = - 831 J

Zgodnie z I zasadą termodynamiki zmiana energii wewnętrznej jest równa:

AU = W + Q , ale AU = 0 skąd Q = -W

Q = - (-831 J)

Q = 831 J

Odp.: Podczas cyklu A-B-C gaz otrzymał 831 J ciepła, wykonując 831 J pracy, ale jego energia wewnętrzna nie uległa zmianie.

Zadanie 686 str.137

Dane:

Odczytujemy z wykresu.

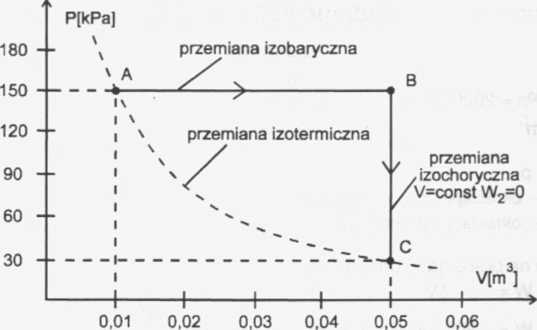
Ze stanu A do C można przejść bezpośrednio w wyniku przemiany izotermicz-

nej bo:

PaA/a = 150 kPa • 0,1 rrł³ = 15 kPa ■ m³ pc • Vc = 30 kPa ■ O.źrrP = 15 kPa ■ m³, więc pa • Va = pc • Vc , Ta = Tc Podczas przemiany izobarycznej A-B gaz wykonuje pracę Wi.

Wi = - pA • AV , ale aV = Vb~Va skąd Wi = - pA • (Vb - Va)

Wi =- 150 kPa ■ (0,05m³- 0,01/t?³)

Wi =- 150000 Pa- 0,0ĄrrP , Pa = ~

rrr

W₁₌-600OĄ-rrP    ,    N-m=J

Wi = - 6kJ