MATEMATYKA021

34 I. Wiadomości wsię/mc

34 I. Wiadomości wsię/mc

<_|'+<oo). Funkcja y=x‘-2x jest ograniczona np. na przedziale

c/ona na zbiorze R, gdyż zbiór wartości lej funkcji jest przedziałem

A=<0,3>,gdyż I £ x² -2x£3 dla x eA.

c) Funkcję f nazywamy monofoniczny na zbiorze A, gdy jest ona rosnąca, malejąca, nicmalejąca lub nierosnąca na A, przy czym

W szczególności funkcje rosnące i malejące nazywamy ściśle mo notonicznymi.

Na przykład funkcja y = cosx jest funkcją malejącą na przedziale < 0,7t >, a rosnącą na przedziale < n,2n >. Funkcja y = x‘ - 2x

jest funkcją rosnącą na przedziale < 1. foo), a malejącą na przedziale (-cc,1 >. Natomiast funkcja Dirichleta

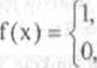
X€ W, x e R - W ,

nie jest funkcją monofoniczną na żadnym przedziale.

Nietrudno zauważyć, że funkcja ściśle monofoniczna na pewnym zbiorzejesf równowartościowa na tym zbiorze.

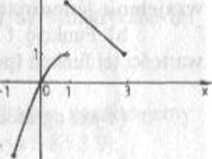
Rys 3.10

Jednak nie odwrotnie. Funkcja równowartościowa na pewnym zbiorze nic musi być na tym zbiorze monofoniczna, o czym przeko-

której wykres przedstawiony jest na rysunku 3.10

f2x - x², - I ś X < I,

[4 - x, I < x £ 3,

FUNKCJA ZI.OŻONA. Załóżmy, że dane są funkcje u \ >U oraz f:U—► R, przy czym XcR i UcR. Funkcję I \ > R określoną wzorem

A F(x) = f(g(x))

x«X

m mywamy złożeniem (funkcją złożoną) funkcji f i g, przy czym funkia I nazywamy funkcją zewnętrzną, u funkcję g-funkcją

•    wnętrz n ą. Funkcję złożoną F oznaczamy też symbolem f o g.

Na przykład funkcja określona wzorem

F(x) - (x^: +x-2)\ x cR.

|r i funkcją złożoną postaci F(x) = f(g(x)), gdzie g(x) = x‘ + x-2,

•    R oraz f(u) = u', u fc R.

FUNKCJA ODWROTNA. Załóżmy, że dana jest różnowartoś-

na    nj

i u>wa fiinkcja f: X—> Y. Funkcję f" : Y—> X taką. że A A (f(y) x o f(x) = y)

x«X ycY

n używamy funkcją odwrotną do funkcji f.

Z definicji lej wynika natychmiast, żc dla każdego x e X mamy r ^ł(f(x)) = x.

Wykresy funkcji y = f(x) i x = f ’(y) są identyczne, natomiast wykresy funkcji y = f(x) i y = f ‘(x) są symetryczne do siebie względem prostej y - x (rys 3.11).

PRZYKŁAD 3.3. Funkcja (1)    y = 4 - x², xe<0,+oo),

jest funkcją różnowurtościową i odwzorowuje zbiór X =< 0, Foo) na zbiórY = (-oo,4 > (por. rys 3.12). Istnieje zatem funkcja odwrotna do tej f unkcji i wyznaczamy ją rozwiązując (1) względem x.