MATEMATYKA037

66 I). Ciągi i izarrgi liczbowe

c) o wyrazach ujemnych i zbieżnego do zera, 0 o wyrazach większych od \ i zbieżnego do I.

3.    Sformułować twierdzenie odwrotne i przeciwstawne do twierdzenia

ciąg(a_n) jest ograino/ony    ciąg (a_n) jest zbieżny.

Które z tych trzech twierdzeń są fałszywe? Odpowiedź uzasadnić podając odpowiedni pr/ykład

4,    /badać monotoniczność ciągu o wyrazie ogólnym a„, gdy:

^c>a"⁼-^rr- ^d)8"⁼ _n

a) a_;) -b)a_r

n    n    I n-n²    n!

n* 11

nTr

5. Wykazać, że ciąg (u_n) nie jest monotoniczny, gdy

a) a„ -cosn. b) a_n *(I‘+(-l)ⁿ)n, c)a_n = (-l) ² n.

n+1

6. Który z ciągów o wyrazie ogólnym a_n: a)a„=(-ir, b)a„ =3‘{^-)°. c)a„=3<-2)\ d)a„ = ~

jest rosnący, malejący, ograniczony, geometryczny, zbieżny?

7.    Ciąg (aj ma granicę a €.(0,1). Obliczyć granice ciągów: a) (aj², b)^a_R, c)(--), d) (a Jⁿ.

n

X. Obliczyć granicę ciągu (aj. gdy;

2n^2 -1	i>) ^an	3n^fc - n	e) an«
a) an ■ ?-, n“ +1		n + 1 '
	e) ^an ^58	^ j^2n i	* 0 a„ =
■^1 u)a » , • n*		4" +9"
, 6^n+2" ot a. = --	• 3“-' +5"	h) a.,	<|>^n -1

4ⁿ - 2*6

2n*l

-2

4n^: - n

Si?+6’

2~" -f 3 • 4^M

+ 2²"*¹

<3>

i)a„=V5n⁷-n² + 2, j) a„ = V2" + 3"-'+2 .

✓

k) a„ ■= n +Vn^: -ł 4 ,    I) a„ » n ->/n^{1 2} +4 ,

ł) a„ - v'n - V» t T,    m) a_u - n - yflir I,

n) a_n-2n-^rr’ n, o) a_n = n(n - Vn² i 2) _t

p) u,, = n(n - Vn² ł 2n), 7 r) u_n =n - Vn^-n² .

n-yjn² - I

^a.. “-/“-■=* ,

? n — \f 4 n ’ 4- n

-)-²\ b) a_B - (3 - — )ⁿ, c) a_r

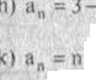
l4 2~" *3 + 4"

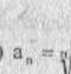
P) ^a"' ~iZT7~T\ ’ ^{r) a}« ln(l + n )

,? .) a„ =    ,t u) a_n = - MM

((n+ I)!)'

(n 4 3)!(2n -1)!

1

+ Vn‘ + 12n ,

2

lnn-n, I) a_n = n~2arcign’,

.n „    ,■ ¹    |

ł) a_n «arcsin—-, m) a_fl narcsino", n) a„ ^~4arctgn,