MATEMATYKA102

194 Ul. Rachunek rótniczknwy

194 Ul. Rachunek rótniczknwy

n^n=R v'«-		1	y»-
		'V .1	V(x^2+n^3
X	-00...	0	.......+00
y		PP

Uwaga. Jest (o funkcja odwrotna do funkcji y«=sinhx, zatem wykresy tych funkcji sq symetryczne do siebie względem prostej y-x

2.

W zadaniu tym podajemy tylko wybrane informacje o badanych funkcjach, a Czytelnikowi pozostawiamy sporządzenie tabel zmienności funkcji i naszkicowanie wykresów.

a) y'=(x-l)^ł(5x+7), y"=4(x-l)²(5x+4)_ł max. lok. dla x=-7/5, min. lok. dla x = l.p. praeg. dla x = -4/5, b) y'=(x+2)²(4x-l).y"=6(x+2K2x + l), min. lok. dla x = l/4, p.przeg. dla x=-2, x=-l/2, c) y^#=~U"^l/x,    ^max

lok. dla x=-l, ^ y-^x-1- ^d) y'»(x³+8)/x³, y"*-24/x⁴, as.: y = x,x=0, max. lok. dla x=-2, e) y' = (8-x²)e ^x, y''=(x²-2x-K)e \ max. lok dla _x -2^2 , mm lok dla x—2^2, p.przeg. dla x=-2, x=4,as. y = 0.

f)    D-i oc 2)^(2,^+ot>)*^{ekslr ,ok} w®. p.JHTeg. dla x*» 1/2, as.^;y = ^e, x — 2.

g)    D-f-ooOMO;**)’ ^max *^{ok dla x=_}^ minm.tok. ^{dlu x = ,}» PP^r7*8^{1 d,a}

x    as.:y*^x* y—*. ^x“^> h)D«(0,+oo), mm lok. dla x-l,max lok.

-i nrzea dla x-c¹^², as X«0, i) y'>0 dla x*0, ekstr lok. nic ma, dlax-= •P,    3-2,nx    .. 2lnx-5

II.. *.±V2. as.y =X, j I)- 0,0,/"    ,y^ł,°-r " — •

pprag .11" *•***'    2V2-tax 4xJ(2-lnx)^y

,    . 2-lnx

max lok. dl« *** '    ^wk,ęsły* ^{k) L>}“^a'*^o)ł    *

„ In²X-21nx-_“ _max. lok dla x-c², p.przeg dla x-c"^\ as. x-l. l)max.

lok dla x*»2/3. ^m'ⁿ lok dla x=0, p.praeg dla x»(2±V2)/3. as. y-0.

. min.lok dla , p.przeg

l)D»(c,+oo),y'

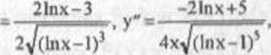
dla x■    ,as. x=e, m)min.lok. dla x«-4/3,as.:y*l, x*(), x=-2,

n)I)»(-oo.O). mm. lok dla x■ -\/Jć. p przeg dla x«-l/cVe, °) D»(0,-ho),

l+x'

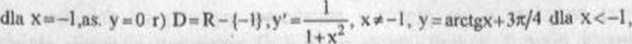
y-orctgx-n/4 dla X>-l, (por. rozxlz III. 4, przykł. 4.4) s) D»R»y' = 0 <M^Q |x|<l, y’ = -4/(l + x²) dla |x|>I, y=0 dla |xj<l, yc-K-4arctgx dla X<-1, y = x-4urctgx dla X>1,a$.:y=x przy x->-oo, y=-x przy x-M-°o,

1+x‘

y = Odla x>0, u) dziedziną jest zbiór dwueleinentowy D»{-1,1}, y(-l)=y(l) = 2, wykres jest zbiorem dwuelementowym: {(-1,2)₍(1,2)}. w) dziedzina jest zbiór jcdnoclcmentowy D = {0}, y(0) = 1, wykres funkcji jest zbiorem jednoelcmntowym {(0,1)}.

3. Z uwagi na okresowość funkcji sin i cos wystarczy zbadać krzywą dla t e<0,2x>. Ponieważ x*(l)#0 dla te(0,~), te(-£,x), t€(*r * ), t€(^,2x), więc na tych

przedziałach równania określają tunkcje postaci y»f(x). Znak f'(x) informuje o monotoniczności. a znak f"(x) - o wypukłości i wklęsłości funkcji f. Krzywa nazywa się nsteroidą i przedstawiona jest na rysunku 8.7.