Matma pochodne

(6.1.15) (arcsin x)' = •===., — 1<x<1, — ire^arcsin . Vi-x²

(6.1.16) (atccosx)' =__=., — 1<x<1 , O^arccosx?g7i.

vl-x²

(6.1.17)    (arctgx)' =-5,    — }rc<arctgx<Jjn:.

1 + x

(6.1.18)    (arcctgjr)' =-r-,    0<arcctgx<n.

1 + x²

(6.1.19)    (**)' = <?*.

(6.1.20)    (fl*)'*a*lnfl, n>0.

(6.1.21)    (ln|x|)'=-, x#0.

x

(6.1.22)    (log,, |xj / = -- —    log_u €, a>0, a# 1, x^0.

xln a x

(6.1.23)    (sinhx)' = coshx.

(6.1.24)    (coshx)' = sinhx.

(6.1.25)    (tghx)'=—L-.

cosh x

(6.1.26)    (ctgh x)‘ =    . ■

sinh x

1

(6.1.27)	(arsinhjt)' = -- - . V 1 + X
(6.1.28)	1 (arcoshx) = -- , xżl. v x^2 -1
(6.1.29)	1 (artghx)=-j, — 1 < x < 1. 1 -x‘
(6.1.301	(arctghx)' =-3, x< - 1 lub 1 — X

We wszystkich wzorach powyższych wielkości «, a oznaczają stale: In x oznacza lo-garytm naturalny, tj. logarytm obliczony przy podstawie e (por. str. 33).

Chcemy obliczyć pochodną funkcji odwrotnej x = aretg y. Korzystając ze wzoru (6.1.8) mamy

dx 1    ,

—-- — = COS‘^lX. dy dy

dx

Prawą stronę przekształcamy na podstawie znanej tożsamości trygonometrycznej

, 1

cos x =

1-Hg²*

i podstawiając tg x—y otrzymujemy

dx 1    1

r-m> ^czy^h (aretg y) =---■

dy l+y²    1+y²

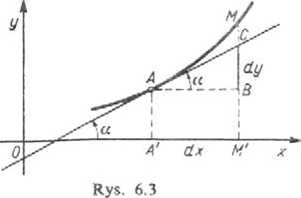
Różniczką dy funkcji y—f(x) nazywamy iloczyn pochodnej tej funkcji przez dowolny przyrost dx zmiennej niezależnej:

(6.1.9)

dy =f'(x) dx.

Różniczka funkcji przedstawia główną część przyrostu funkcji.

Na rysunku 6.3 różniczka BC przedstawia główną część przyrostu funkcji BM, odpowiadającego przyrostowi argumentu dx.

Różniczka funkcji znajduje często zastosowanie w przypadku, gdy wielkości występujące we wzorze, pochodzące z pomiarów, nie są dokładne, lecz podane z pewnym błędem. Wówczas błąd wielkości obliczonej ze wzoru daje się wyznaczyć za pomocą różniczki. Wymienimy ważniejsze wzory rachunku różniczkowego:

(6.1.10)    (x‘)'=ax^a~^l,    x>0, a - dowolna liczba rzeczywista.

(6.1.11)    (sinx)' = cosx.

(6.1.12)    (cos x)' = - sin x.

(6.1.13)    (tgx)'=—ir- = l+tg²x, cosx/0. cos X

(6.1.14)

(ctgx)' = --V = -(1 +Ctg²x), sinx#0. sin x