284 (11)

11. Ciągłość i pochodna funkcji

11. CIĄGŁOŚCI POCHODNA FUNKCJI

11.1.1- Granica ffunkcii (VI)

(3) Interpretacja geometryczna właściwej granicy funkcji w nieskończoności: lim f(x \ = c,

*-*«■ ^v 1    * ~ ^asymptot\

poziome wykresu:    ^J

=8

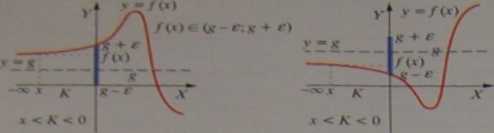
„Czerpiąc” argumenty x dostatecznie małe, ( .v < K < O ), mamy pewność, że wartości funkcji (w tych argumentach) należą do otoczenia r-owego liczby r.

= 8

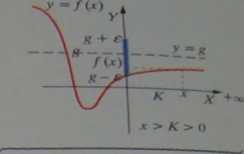
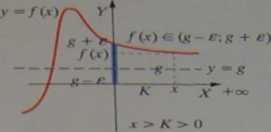
„Czerpiąc” argumenty * dostatecznie duże, ( x > K > 0 \ mamy pewność, że wartości funkcji (w tych argumentach) należą do otoczenia c-owego liczby g.

Wtedy wykres funkcji ma w — co lub w +oo asymptotę poziomą (prostą) o równaniu: y = g.

Uwaga 1: Mogą zachodzić alternatywnie następujące przypadki asymptoty poziomej: y = g:

1° Asymptota pozioma w — oo: lirn^/ (;c ) = g    2° Asy mp to ta pozioma w +oo: lim f(x ) = g

y.	y «/(*> ^Y g \ w >!=£.	vfi*y ^y=f^S\^Y
y="i	\ V__	s r ~ v /	V
			g -y-8
		\J ^x J	X +00

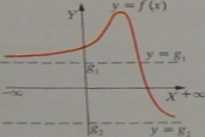
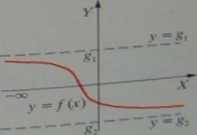
3° Asymptota pozioma w —oo i w +oo:

Jl™₀/(^x) = 8_l

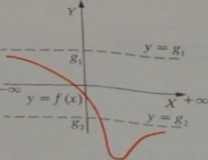
= 82

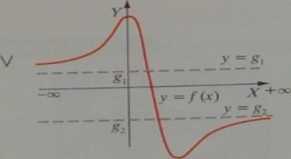
Oczywiście może być: g, = g_r

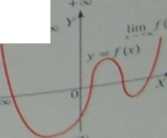
Uwaga 2: Asymptoty poziomej brak, gdy. j-_m    _ _{+ 00}-

Y lęĘ	Im f(ir) y/ujl \ I
-7 ^0 li«n /(i) "-ot	VJ *+

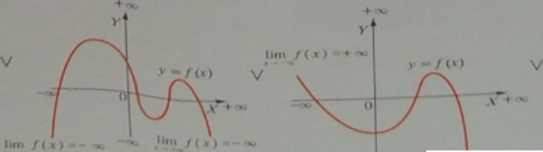
lim /(■<)■""*

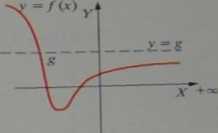
V

lim /(■*> ^{,+ ł}