283 (7)

11.1.1. Granica funkcji (V)

|l)Ptfinię|att1a<ciw«J granicy funkcji w (±oo): lim/(^) = g:

według Heinego:

według Cauchy’ego:

lipy
+ linj.v,^= (-)^00	* JiTŁf (*«)** ciąg odpowiednich	A V A e>o > .*«/>, *(<)°

dwwlny ciąg

nrgumcnuVw jesi rwrNciny

wartości funkcji jest zbieżny do g

dowolne argumenty si) większe (mniejsze) od pewnej liczby dodutniej (ujemnej)

wartości funkcji w tych argumentach si| w otoczeniu ff>owym liczby g

do/

por.:.

por.: Ilrn/(x,) = #

Definicja niewłaściwej granicy funkcji w nieskończoności (±co): lim /(*) = ±oo lim f(x) =+oo V lim f(x) =-oo

^r"(-)“    *-(^:r

skrócony zapis 4 przypadków: lim f(x) = t\°o

mm

według Heinego:

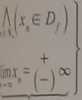
Au*)’ciąg irjumcntów pi rozbieżny

ciąg odpowiednich wartości funkcji jest rozbieżny do

+

według Cauchy’ego:

A    V A

>    > xeD_r

*(<)

K

>/(*)(<)

M

dowolne argumenty są większe (mniejsze) od pewnej liczby dodatniej (ujemnej)

wartości funkcji w tych argumentach są większe (mniejsze) od pewnej liczby dodatniej (ujemnej)

do

[-)

x

00

11. CIAGŁOSC I POCHODNA FUNKCJI

lilagoras (572-497 p.n.e.) -Rdi matematyk, filozof, stójnel słynnej szkoły pi-Jptjskicj, Był także twór-5 kieronku filozoficznego ?ugoreizmu), inicjatorem *u o orientacji religijnej 'tarożytnej filozofii grcc-^Plzyjąl się także pogląd,

¹ Pitagoras przeszczepił ³ bum grecki geometry cz-¹¹¹ astronomiczne umiejęt-Egipcjan i Babilończyków oraz że zainicjował naukowe, uwieńczone szeregiem znakomi-^osiągnięć. Do osiągnięć tych należy między in-^Morzenie początków teorii liczb, sformulowa-*t»icrdzeniu Pitagorasa oraz koncepcja harmonij-**> kosmosu.

Prąd filozoficzny, którego inicjatorem był Pitagoras, trwał ponad dwa wieki, a jego relikty dają się zauważyć jeszcze w pierwszym wieku naszej ery. Dziś niestety trudno dokładnie ustalić, co szkoła pitagorejska zawdzięcza swemu mistrzowi, a co jego uczniom. Dlatego też mówić raczej należy o dokonaniach pitagorej-czyków i nic przypisywać wszystkich odkryć samemu tylko założycielowi szkoły. W zakresie geometrii pita-gorejczycy stworzyli teorię równoległych wraz z twierdzeniem o sumie kątów trójkąta, czworokąta i wielo-boków foremnych, któtych całą płaszczyznę poktyć można tylko trójkątami, kwadratami albo szcścioką-tami; interesowali się także teorią liczb.

W szkole pitagorejskiej narodziły się trzy wielkie problemy: podwojenie sześcianu, podział kąta na trzy równe części oraz kwadratura koła, które należało rozwiązać za pomocą cyrkla i linijki (bez podziałki).