całki funkcji cyklometrycznych
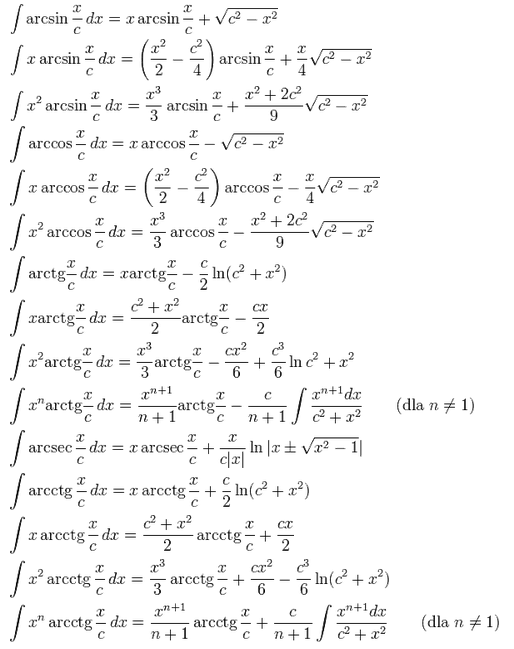
/
/
/
/
arcsin — dx = x arcsin — + Vć* — x2
c c
. X . (x2 c2\ . X X -
x arcsin - dx = I —---- I arcsin — + — v c2 -
c \ 2 4 / c 4
o . x x3 . x x2 + 2c2
x arcsin — dx = — arcsin — H----
c 3 c 9
arccos — dx — x arccos -— \Jc2 — x2 c c
x*
x
J x arccos — dx = ^^ arccos — — — n/c2 — x2
+ 2C2
/
/
/
/
/_ x , xn+l x c f:
x arctg— ax =-arctg---/ -
c ?i+l c n + 1 ./ <
/
/
/
/2 X , X3 X CX2 C3 , . 2 2\
x arcctg — ax = — arcctg — + —--— ln(c + x )
h"
2 x x° x
x arccos — dx=— arccos--
c 3 c
00 C
arctg— dx = rrarctg-— - Infc2 + x2) c c 2
xarctg —dx =
C2 + X‘
X cx arctg- - y
X cx
2
\Z(? — X‘
2 X X .Ł ut t 2 9
x arctg— ax = —arctg---— + — In c + x
c 3 c 6 6
<? + x'
(dla 77 ^ 1)
arcsec — dx = x arcsec —|- r ln |x ± vx2 — 11
c c c\x |
00 00 c
arcctg — dx = x arcctg — + - Infc2 + x2) c c 2
x arcctg — dx =
c2 + x:
X cx arcctg - + — c Ł
x , xn+1
arcctg — dx = -
c Ti + 1
c 6 arcctg
x c f 5
C 77 + 1 ./ <
C2 + X2
(dla 7?1)
Wyszukiwarka
Podobne podstrony:
Funkcje cyklometryczne: arcsin i arccos Funkcja arcsin to funkcja odwrotna do sin /_* ,1, czyli do f
172 2 342 XVII. Całki funkcji niewymiernych Łatwo obliczyć, że = lnx-+j x2-2x. dx y/x2-2x Mamy więc
167 2 332 XVII. Całki funkcji niewymiernych a następnie(3) Ze wzoru (2) obliczamy(4) /x2 +k-t-x=t— t
175 2 348 XVII. Całki funkcji niewymiernych 17.79. J n/V-4 dx . 17.81. J Vx2-3x+2tfx. 17.80. J y[3x2
Matma pochodne (6.1.15) (arcsin x) = •===., — 1<x<1, — ire^arcsin . Vi-x2 (6.1.16) (atccosx)
skanuj0004 Całki funkcji elementarnych: Całki: Odpowiadające pochodne. ja dx - a jdx = ax + C (ax
19 (4) Biblioteczka Opracowań Matematycznych jVl -4.r2dx = j^4^-x1 jdx = 2 jj^-x2dx =^arcsin 2x + x^
104(1) 491. 493* i e° sin bxdx ln xdx J 492*. f^nXdx 494*.
19 (4) Biblioteczka Opracowań Matematycznych jVl -4.r2dx = j^4^-x1 jdx = 2 jj^-x2dx =^arcsin 2x + x^
322 XVI. Całki funkcji wymiernych Wykonujemy podstawienie x—2 = sj91, skąd dx—3dt. Podstawiając
161 2 320 XVI. Całki funkcji wymiernych Podstawiając wartości (3) i (4) do (1) mamy ostatecznie /’2x
174 2 346 XVII. Całki funkcji niewymiernych gdzie — 1<m<0 lub 0<w<l. Stąd 1 x2 = - u du
354 XVIII. Całki funkcji przestępnych Wykonując podstawienie tg ix=u(1), skąd dx 2 cos2 = du,
więcej podobnych podstron