162

322 XVI. Całki funkcji wymiernych

Wykonujemy podstawienie x—2 = _sj91, skąd dx—3dt. Podstawiając mamy

322 XVI. Całki funkcji wymiernych

f dx    r 3dt 3 r

J (x² — 4x + 13)²~ J (9t²+9)²~9¹j

dt

1

(t² + l)² 27

Opierając się na zadaniu 16.22 piszemy +i arctg f=

x- 2 3

A* “2

^/2=2 • ^Tfj+ł ^arct8 <=1    +1 arctg —

jc-2

² ;c² —4x +13

. i    *-•>

+ 2 ^arctg —:

3

Ostatecznie więc mamy dx

f _=_lA

J (x²-4x + 13)^{2 27} V²

x—2    .    x-2\

+i arctg -y-) + C =

x²-4x + 13 x — 2

¹⁸ x² — 4x + 13⁺** ^arctg ₃ +^c•

Zadanie 16.24. Obliczyć całkę

dx

J x(x²+2)³ ’

Rozwiązanie. Zakładamy, że x#0. Rozszerzamy funkcję podcałkową mnożąc licznik i mianownik przez x:

xdx

j x²(x²+2)³

i wykonujemy podstawienie x² = t; wtedy t> 0, a różniczkowanie daje xdx=\dt. Otrzymujemy więc

f *    f_*_

J x(x²+2)^{3 2} J r(r + 2)³'

Funkcję podcałkową rozkładamy na sumę ułamków prostych

,    _1_₌ A B CD

t(f+2)³~ t ⁺(f+2)³⁺(/+2)^{2 +} f+2 ’

skąd otrzymujemy

ls/ł(l+2)³ + Bf+ Ct(f+2) + Dr(r+2)² .

W miejsce i podstawiamy kolejno pierwiastki mianownika; gdy r=0, to A = \, a gdy t=— 2, to B= Mamy więc

l=|(r³+6r² + l2r+8)-|r+Cr(i+2)+Z)r(r+2)².

Po przeniesieniu wyrazów o współczynnikach liczbowych na lewą stronę otrzymujemy

-~t³-2t²-t = Ct(t+2) + Dt(t+2)² .

Widzimy, że prawa strona tożsamości dzieli się przez z (t+2), a więc lewa strona musi dzielić się przez to samo wyrażenie; po podzieleniu obu stron mamy

—f t—j=C + D(f+2) ,    czyli    -'._t-± = Dt+(C+2D),

skąd porównując współczynniki otrzymujemy D=—    C=—£.

Tożsamość (1) przyjmie teraz następującą postać:

i    i    i    ii

¹ 8    -    T    -

f(t+2)³

t

Całkując otrzymujemy

(t+2)³    (t+2)²    t+2

f -li	r*-*j	r * *i	r * ii	1
I t(t+2)^3 8J		1 (t+2)^3 4J	1 (t+2)^2 8 J	1 t+2

=4 ln t—4 •-—=-

^{8    2} 2(f+2)²

-1

7+2

1

-±ln(f+2)=

—4 ln--1--■- + •

⁸    t+2 4(r+2)² 4(f+2)'

Wracając do pierwotnej całki i podstawiając t=x² otrzymujemy

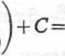
dx _i A x²    1    1

x(x²+2)^{3 2}\^{8 n} x²+2⁺4(x²+2)² +4(x²+2)

i²    1    1    ^

?+2⁺8(^²+2)^{2 +} 8(^+2) ^{+ C}'

Zadanie 16.25. Obliczyć całkę

x⁶ - 6x⁵ +10x⁴ — 17 x³ + 8x² - 5* +1 (x⁴+2x² +1) (x⁴ - 3x³ + 3x² - x)

Rozwiązanie. Zauważmy, że mianownik funkcji podcałkowej możemy przedstawić w postaci x(x-1)³ (x² +1)². Zakładamy, że x¥=0, x#l, i przedstawiamy funkcję podcałkową w postaci sumy ułamków prostych

- 6*⁵ +1 Cbc⁴ -17x³ + 8x² - 5*+1 ^{2 1}

1

Sprowadzając do wspólnego mianownika mamy / - 6x⁵ + 10x⁴ - 17x³ + 8x² - 5x +1 =

sA(x-1)³(*² + 1)²+.Bx(x² + 1)²+Cx(x-1)(*² + 1)² +

+ Dx (x -1)² (x² +1)² + a: (Ex + F) (* — l)³ + x (Gx+H) (x-1)³ (x² +1) .

U*

2

(x*+2x² + l) (x⁴ - 3x³ + 3x² - x)

₌ A B    C D Ex+F Gx+H

x ⁺(x-1)³⁺0-1)^2T;c-1 V + D²⁺ x² + l