3818438110

Całki funkcji wymiernych

I^ldx

I xⁿdx — -J    7\

.71 +1

Tl + 1

/(aa-+ 6)” dr-

(n + -1) (a# + 6)ⁿ⁺¹ a(n +1)

(dla n ^ —1)

I —d:r = ln \x

J X

f —da? =

J xⁿ

I=

-i

oj: + 6

(n — l)j;^ra-1

= — ln Ioj: + 61 a

{n ± 1)

/x(ax + 6)"da =    + 6)"⁺¹ (dla n £ {-1, -2})

x dj:    x b

/    ~ , = ----^ ln Ioj; + 61

f x dx    b    1

J JaxTW ⁼ «²(aa + 6) ¹    “ ^ ¹ ^

f x dLr    a(l — n)x — b

J {ax + 6)” a²(n - l)(n — 2)(oj: + 6)^71-1

(dla n <£ {1,2})

x dj*

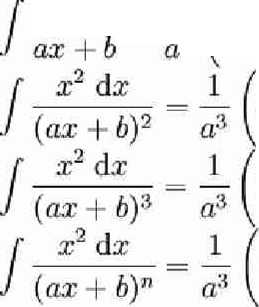
oj: 4- b — 26 ln |or + 6|

ln |ax + 6| +

1_ ^ [ tu \ 6)--2b(ax + b) -|- 6² ln \ax -I b\

2

26

ax + 6

b²

ax + 6    2 (oj: + 6)²

1 26

+

(n — 3)(o:r + 6)^n_:ł    (77. — 2) (o + 6)ⁿ~² (n — 1) (ax + 6)

n —1