P1080225

4. Wprowadzenie do kinematyki robotów

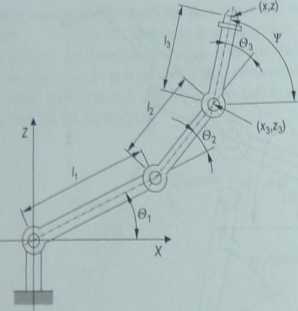
Rysunek 4.12__

Robot o trzech stopniach swobody w przestrzeni dwuwymiarowej

Współrzędne w przestrzeni dla końca ramienia są opisane układem równań 1

X = /|COS(9| + /2COS(@i + ©2) + /jCOS(0i +02+03)

r = pin@i + /2sin(0i + 02) + /jsin(0i + 02 + 03)    (4.24) 1

^ = (^ + 02 + 03)

Korzystając z wyników dla robota o dwóch przegubach, można wyznaczyć I transformację odwrotną dla robota o trzech stopniach swobody. Do zdefiniowa I nia pozycji końca ramienia użyte będą oznaczenia x, z, ¥'. Kąt H^J oznacza or\ev I tację kąta nadgarstka.

Mając te wartości, można obliczyć 0\ + 0₂ + ©3, wprowadzając

Xj^S8Jt-/)C0s!f'

rj=2 - /jsin V⁷    ,. ^    _t

Mając ustaloną pozycję trzeciego przegubu, problem ustalenia \ sprowadza się do przypadku robota z dwoma stopniami swobody, który by, lizowany wcześniej.

4.23.4. Robot z czterema stopniami swobody w przestrzeni o trzech wymiarach

Na rysunku 4.13 pokazano konfigurację robota o strukturze (£r, Ar\. % w przestrzeni o trzech wymiarach.

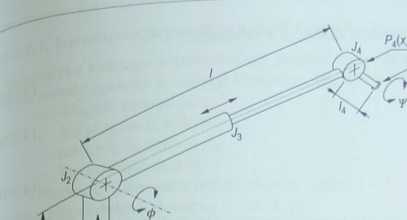
Rysunek 4.^________

Robot o czterech stopniach swobody i strukturze (C*. A_K,, Y_R, Am) w płaszczyźnie trójwymiarowej

Robot ma 4 stopnie swobody: przegub J\ umożliwia obrót wokół osi Z, przegub Jj - obrót wokół osi X, para kinematyczna Ą jest połączeniem liniowym, umożliwiającym przemieszczanie wzdłuż osi Y, przegub J4 umożliwia obrót wokół osi X (równoległej do osi przegubu J2).

Kąt ©jest kątem obrotu przegubu J\₉ kąt 0 obrotu przegubu jest kątem wznoszenia, długość liniowego połączenia J$ - rozciągnięciem L kąt *P obrotu przegubu Ją tworzący płaszczyznę YZ - kątem skoku. Oznaczenia te pokazano na rys. 4.13.

Pozycja P końca ramienia jest określona w przestrzeni następująco

(4.26)

4.2. Kinematyka robotów o strukturze szeregowej

Z

P4fa.y4.Z4)

x ® (/coscP+ /₄cos \P) cos© y - (/cos<P + /₄cos !P)sin<9

z = li + /sin O + /₄sin *F

Znając położenie punktu P(.\\ y, z) i kąt skoku P. można znaleźć pozycję przegubów w przestrzeni. Dla punktu P₄(.v4, v₄, r₄), który jest pozycją przegubu A w przestrzeni, otrzymuje się

*4 ** x - /₄cos fPcos <9

H ^m y -I /4COS ^sin <9    (4.27)

z₄ ® z - /₄sin *P    9