P1080223

4. Wprowadzenie do bnematyłri robotów

Rysunek 4^_______

Przesunięcie określające pozycję punktu P w układzie {B} względem układu {.-4}

Odwzorowanie obrotu układu współrzędnych

Opis wektora względem układu {B} jest znany, szukany zaś jest opis względem układu {A} - iys. 4.8. Oznaczmy: ^BP - opis wektora P względem układu {B). *P- opis wektora P względem układu {A}

» W

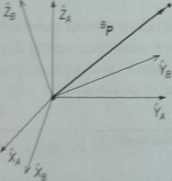
Rysunek 4.3____

Opis wektora ^eP względem obróconego układu współrzędnych

Wektor ^BP względem obróconego układu współrzędnych opisuje się za pomocą składowych ^AP_t. Składowe wektora ^AP odpowiadają rzutom wektora P na osie współrzędnych układu {A). Składowe te znajduje się z iloczynu skalarnego

^AP_x = ^BX_A^BP

(4.1

^aPz = ^bZ_a^bP

Stąd

92

gdzie gR - macierz obrotu.

Uogólniony przypadek odwzorowywania układów

Przesunięcie i obrót określające pozycję punktu P w układzie {/?} względem układu {A} zilustrowano na rys. 4.9.

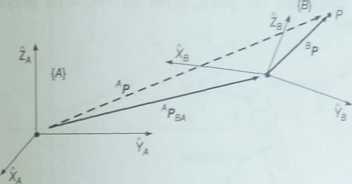
Rysunek 4.^_____

Przesunięcie i obrót określające pozycję punktu P w układzie [B) względem układa {A)

Ogólne przekształcenie odwzorowujące opis wektora względem jednego układu w opis względem drugiego układu, uwzględniając przesunięcie między początkami układów współrzędnych, określa wzór

^aP=ŚR^bP + ^aPborg    (4.13)

4.2.3. Opis kinematyki w notacji geometrycznej

4.2.3.1. Transformacja prosta ramienia o dwóch stopniach swobody

Dla dwuwymiarowego robota o dwóch stopniach swobody pokazanego na rys. 4.5 można ustalić pozycję końca efektora w przestrzeni, definiując wektory

dla ramienia li i dla ramienia l₂

r\ = [/icos&i, /isin6>i]    (4.14)

f2= [/₂cos(<9i + 02), /_;sin(6>i + 6?>)]    (4.15)

Po dodaniu wektorów (4.14) i (4.15) otrzymuje się współrzędne x. z końca efektora w przestrzeni

x—/|Cos6>i +1₂ cos(6>i + 0>)    (4.16)

z = /isin6>i +i /₂sin(0| + 0?)    (4.17)

4.2.3.2. Transformacja odwrotna ramienia o dwóch stopniach swobody

W wielu przypadkach jest znacznie ważniejsze, aby znając kąty obrotu w dwóch przegubach, znaleźć położenie końca ramienia w przestrzeni. Typowa sytuacja występuje wówczas, gdy operator musi policzyć te kąty, aby przesunąć efektor do punktu w przestrzeni zdefiniowanego przez jego współrzędne. Dla robota 93